
作者:逸柳的知行之路
博弈论是研究少数几个主体进行策略性互动的学科。策略性互动的核心在于,每个人在决策的时候,都不仅考虑现有的情况,还要考虑到自己决策对另一方决策的影响。其中在教科书和课堂上必然会讲到的案例就是囚徒困境(prisoners' dilemma)。
囚徒困境是关于两个犯人被警察抓获,然后在相互隔绝的环境下被提审的故事。现在我们假设有两个人某甲、某乙一起合伙犯罪,然后被警察抓住了,被分别关在两个牢房里。
于是警察对某甲说:“现在的证据足以让你们两个被判1年有期徒刑,但是我们还想给你几个选择。如果你承认自己的罪行,指认你的同伙,而你的同伙不招供,那么你立刻就获得自由,可以回家去陪老婆孩子,而你的同伙将被判10年有期徒刑;如果你们两个人都招供,你们都将被判5年;如果你一定要嘴硬,而你同伙招供了,那不好意思,你要去吃10年牢饭。”
对于某乙,警察也是同样的说辞。
现在,我们将两个犯人的选择和判刑年数做成一张表。这个表可以称为收益矩阵(payoff matrix)。
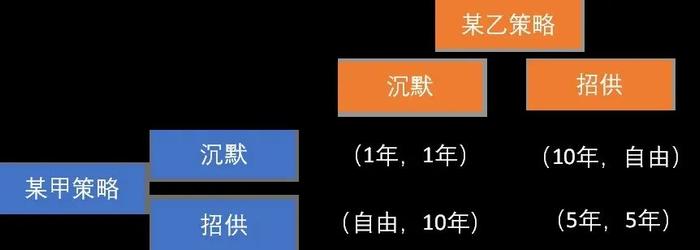
这里我们可以看到,假定某乙决定沉默,那么某甲选择招供是最好的选择,因为马上就可以获得自由;而如果假定某乙决定招供,选择招供依然是更优的选择,因为避免可以被判10年的处境。这样一种无论其他参与者选择什么策略,对于特定参与者而言,都是最优选择的策略,我们称其为占有策略(dominant strategy)。在囚徒困境案例中,招供对于某甲而言就是占有策略,对于某乙而言同样如此。
占有策略是非常严格的,因为要求对某乙所有的策略,某甲的策略都是最优的。
所以又引入了一种博弈下的平衡概念。如果给定B的策略选择β,A的策略选择α是最优的;同时对于B而言,当A的策略为α时,B选择β策略也是最优的,这样的话,就能够达成一个均衡状态,也就是博弈论中所说的纳什均衡(Nash Equilibrium)。
纳什均衡是以美国数学家约翰·纳什(John Nash)命名的,电影《美丽心灵(A beautiful heart)》就是以纳什的事迹作为蓝本。
在囚徒困境中,(招供,招供)这样的策略组合就是一种纳什均衡,为什么呢?因为给定某乙的决策是招供,某甲的最优选择是招供;对于某乙也是如此。
而(沉默,沉默)这个策略组合,虽然两个人的收益比(招供,招供)更高,但是却不是纳什均衡。给定某乙的决策是沉默,某甲的最优选择,很不幸,是招供;对于如果某甲的决策是沉默,某乙的最优选择也是招供。
因此,囚徒困境之所以称为是困境,因为无法达成对双方都最优的选择。
博弈中,纳什均衡不一定只有一个,可能会存在多个纳什均衡,还有可能不存在纳什均衡。
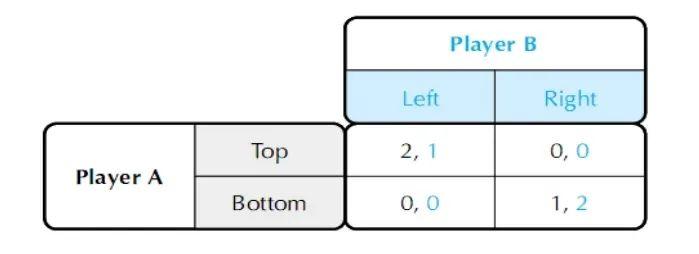
比如我们看下面的收益矩阵,A玩家如果选择“上”,B玩家选择“左”,那么A得到2块钱,B拿到1块钱,而假如B选择“右”,则两个人什么都得不到;A玩家如果选择“下”,B玩家选择“左”,两个人都什么也得不到,而如果B玩家选择“右”,则A得到1块钱,B得到2块钱。
这种情况下,(上,左)和(下,右)都是纳什均衡。只是两个纳什均衡带来的利益关系不同,A玩家更喜欢(上,左)这样的均衡,而B玩家更喜欢(下,右)。
囚徒困境是一种一次性博弈,但是在经济生活中,往往存在重复博弈,如果按照我们最初的某甲、某乙的博弈矩阵,只是将其由现实中的犯罪变成一个囚徒博弈游戏,把判刑变成罚钱,从而能够无限重复下去,那么可能不用多少次,某甲和某乙就会达成“沉默”的策略默契,因为一方背叛后,另一方下一次也会背叛,给予对方惩罚,从而在之后的博弈中都得益更少。无限博弈中,更有可能达成合作的情况。
但是如果介于一次和无限之间,也就是有限的多次博弈,那么在临近博弈结束的那几次,合作可能会变得脆弱。
囚徒困境这样的博弈模型可以加入更多的条件,变得更加复杂,比如可以加入概率的因素,也就是混合博弈,一方用某个概率选择α1策略,用另一个概率选择α2策略。但是复杂的博弈,基本上都是简单博弈的变种。
研究博弈的基本逻辑在于首先要知道策略选择的集合,然后要知道各方的收益矩阵,这样就可以大概知道对方会采用什么样的决策。


