主要
观点
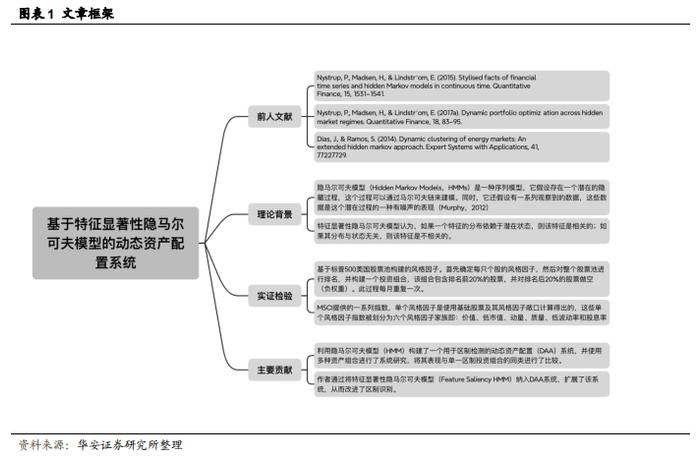
本文使用隐马尔可夫模型(Hidden Markov Models,简称 HMMs)构建了一个动态资产配置模型。作者测试了该模型在多种 smart beta 策略组合下的表现,结果表明,所得投资组合的风险调整后收益有所改善。此外,作者还提出了一种基于特征显著性隐马尔可夫模型(Feature Saliency HMM,简称 FSHMM)算法的新型 smart beta 分配策略,该系统在进行隐马尔可夫模型训练的同时进行特征选择,以提高状态识别的准确性。回到 A 股市场,HMM 大多用于宏观经济周期的识别,本文的做法值得参考。
基于 HMM 动态资产配置模型所得投资组合的风险调整后的收益有所改善
作者证明,通过采用一种基于隐马尔可夫模型的投资组合构建策略,该模型包含两个潜在状态并特定地训练于将要进行配置的资产之上,相较于传统单一状态方法构建的组合而言,能够显著提升投资组合的绩效。进一步的,作者通过计算不同类型的投资组合对此进行了测试。对于收益导向型和平衡型投资组合,这种改进更为显著;而在更注重风险的投资组合中,这种改进则不太明显。
基于 FSHMM 构建的新型 smart beta 配置策略表现更佳
作者使用隐马尔可夫模型算法从一组因子指数中选择相关特征,并将其与使用全部资产训练的 HMM 进行了比较。两个模型在状态识别上均表现出一致性,而仅使用相关特征训练的模型对经济困境时期的敏感度更高。
作者通过 MSCI 美国增强因子指数,使用真实、可投资的资产对两个模型进行了测试。与使用全部特征训练的 HMM 相比,使用经过相关特征训练的 FSHMM 的信息构建的投资组合表现更佳。
文献结论基于历史数据与海外文献进行总结;不构成任何投资建议。

1
引言
“Smart beta”是一个相对较新的术语,近几年来在资产管理领域变得无处不在。Smart beta 背后的金融理论被称为因子投资,自 20 世纪 60 年代便已存在,当时人们首次发现因子是股票回报的驱动因素(Agather 和 Gunthorp,2017)。这些因子回报可能是风险的来源,也可能是提高回报的途径,因此,了解任何额外风险是否能够通过更高的回报得到充分补偿非常重要(Ang,2014)。
主动管理型基金经理通过根据股票的因子暴露来选择股票,可以构建具有特定因子暴露的投资组合,从而利用因子投资来提高投资组合回报或降低风险,具体取决于他们的特定目标。Smart beta 旨在通过采用透明、系统化、基于规则的方法,以较低的成本实现这些目标,与主动管理相比,这种方法能够显著降低成本(Asness,2016)。
尽管长期来看,smart beta 策略表现强劲,但它们往往会在周期波动中经历严重的短期回撤(峰值至谷底的下跌)(Arnott 等人,2016)。这些波动可能源于极端宏观经济状况、波动率上升、多个市场之间的相关性增强,以及货币和财政政策响应的不确定性。在本文中,作者通过构建使用隐马尔可夫模型(Hidden Markov Models,HMMs)的区制转换模型来解决这一问题。隐马尔可夫模型已成为时间序列数据建模的主流技术之一(Baum 等人,1970;Rabiner,1989),并广泛应用于语音识别、文本分类和医疗应用等多个领域。作者首先研究如何使用区制转换框架来检测各因子之间的区制,以及这样做是否能为 smart beta 策略提供增量。在资产配置的区制转换框架中,普遍的做法是预先指定一个依赖于预测状态的静态决策规则(Nystrup 等人,2017a)。另一种方法是利用推断出的区制参数信息动态优化投资组合。作者遵循第二种方法,利用区制信息构建不同类型的投资组合(更注重收益和更注重风险)。第一步,作者建立一个动态资产配置(Dynamic Asset Allocation,DAA)系统,通过区制转换模型构建投资组合,并使用与投资组合分配相同的因子训练 HMM,从而对数百种因子组合进行系统分析。作者的研究表明,使用 HMM 的区制信息比单一区制分配的表现更好,作者发现更注重收益的投资组合的风险调整后收益优于其基准,而更注重风险的投资组合的表现也有所改善。最后,金融领域大多数关于区制转换模型的研究的共同点是,它们要么考虑单个资产,要么考虑一小组资产来构建模型,而资产的选择标准通常来自经验。这是因为 HMM 的无监督特征选择非常有限,包装方法计算成本高,或者针对 HMM 的方法很少(Adams & Beling,2017)。在大多数 HMM 应用中,特征要么是基于专门知识预先选择的,要么完全省略了特征选择。Adams 等人(2016)提出的特征显著性隐马尔可夫模型(Feature Saliency Hidden Markov Model,FSHMM)是为 HMM 开发的少数特征选择算法之一,其中特征选择过程嵌入到 HMM 的训练中。作者将这种 FSHMM 纳入作者的动态资产配置系统,带来了两个好处:(1)通过在训练过程中选择特征,作者期望通过选择状态依赖的特征并拒绝状态独立的特征来改善区制识别;(2)它允许在模型中加入许多特征,并让算法决定哪些特征有助于区制识别,从而避免在构建金融周期时需要专门知识。
本文的主要贡献如下:
1.作者利用隐马尔可夫模型(HMM)构建了一个用于区制检测的动态资产配置(DAA)系统,并使用多种资产组合进行了系统研究,将其表现与单一区制投资组合的同类进行了比较。作者证明,DAA 系统的表现始终优于基准;
2.作者通过将特征显著性隐马尔可夫模型(Feature Saliency HMM)纳入 DAA系统,扩展了该系统,从而改进了区制识别;
作者使用摩根士丹利资本国际(MSCI)指数对嵌入特征选择的 DAA 系统进行了实际可投资指数的测试,并证明与使用未进行特征选择的 DAA 系统构建的策略相比,使用带有特征显著性隐马尔可夫模型(FSHMM)的 DAA 系统构建的策略在风险调整后收益方面有所改善。
本文的组织结构如下:第 2 节概述了隐马尔可夫模型在金融领域的先前研究;第 3 节介绍了隐马尔可夫模型和特征显著性隐马尔可夫模型;第 4 节描述了数据和指数构建;第 5 节介绍了动态分配系统、特征显著性算法及其在动态资产配置系统中的应用;第 6 节展示了 DAA 系统的回测结果以及嵌入特征选择的应用。最后,作者使用可投资资产对带有特征选择的 DAA 系统进行了测试;第 7 节为结论和后续展望。
2
相关文献
在金融领域,自 Hamilton(1989)提出使用区制转换模型通过国民生产总值(GNP)系列来识别经济周期以来,隐马尔可夫模型(HMMs)已被广泛用于建立基于区制的模型。正如 Ang 和 Timmermann(2012)所指出的,HMMs 可以同时捕捉金融收益序列的多个特征,如时变相关性、偏度和峰度,即使在底层模型未知的过程中也能提供良好的近似(Ang 和 Bekaert,2003;Bulla 等人,2011;Bulla 和 Bulla,2006;Nystrup 等人,2015,2017b)。此外,HMMs 的结果具有良好的可解释性,因为从区制的角度思考是金融领域的自然方法。动态资产配置的例子包括 Reus 和 Mulvey(2016),他们使用 HMM 构建了一个使用货币期货的动态投资组合,以及 Bae 等人(2014),他们使用 HMM 来识别不同资产类别的市场区制,区制信息有助于投资组合在左尾事件中避免风险。
Guidolin(2012)对马尔可夫转换模型在实证金融中的应用进行了广泛回顾,涵盖了股票收益、无违约利率的期限结构、汇率以及股票和债券收益的联合过程。在资产配置之外,HMMs 还被用于捕捉能源价格动态(Dias 和 Ramos,2014),构建信用风险系统,例如 Petropoulos 等人(2016)使用学生 t 分布的 HMM 构建了一个信用评级系统,解决了当前系统的两个问题:其重尾的实际分布和其时间序列性质;Elliott 等人(2014)使用双重隐马尔可夫模型构建了一个模型,以提取关于公司真实信用质量的信息。Dabrowski 等人(2016)研究了 HMMs 和其他贝叶斯网络,以构建检测系统性银行危机的预警系统,并发现贝叶斯方法在预警方面的性能优于传统的信号提取逻辑模型;Zhou 和 Mamon(2012)研究了三种流行的短期利率模型,并将其扩展为使用有限状态马尔可夫链来捕捉经济区制的转换。
到目前为止,关于区制转换模型对因子投资的影响的研究还很少。其中,Guidolin和 Timmermann(2008)发现了规模和价值因子中存在四个经济区制的证据,这些区制捕捉了平均收益、波动率和收益相关性的时变特征。Liu 等人(2011)和 Ma 等人(2011)使用六因子模型来研究时变风险溢价,以解释行业交易所交易基金(ETF)的收益。在他们的研究中,测试时间较短(9 个月),并且没有考虑交易成本。
3
理论背景
3.1 隐马尔可夫模型(HMMS)
隐马尔可夫模型(Hidden Markov Models,HMMs)是一种序列模型,它假设存在一个潜在的隐藏过程,这个过程可以通过马尔可夫链来建模。同时,它还假设有一系列观察到的数据,这些数据是这个潜在过程的一种有噪声的表现(Murphy,2012)。简单来说,HMMs 就是通过观察到的数据序列来推断出隐藏的马尔可夫过程的一种模型。
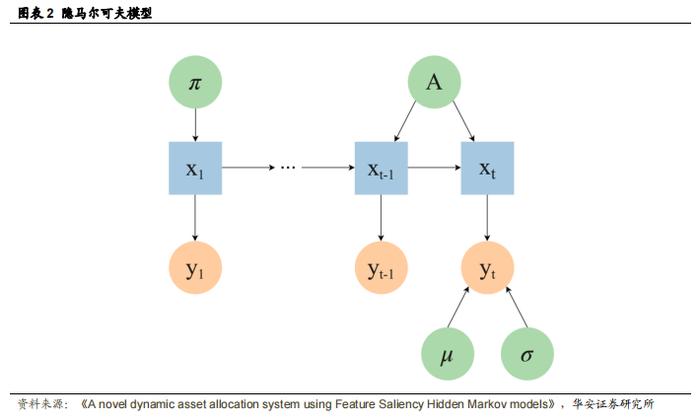
给定观测数据序列σ = {y1, .. . , yt},其中每个xt ∈ RL,L 为观测数据的维度,x = x1, . . . , xt为潜在状态序列,其中xt ∈ {1,...., K},K 为潜在状态的数量。隐马尔可夫模型(HMM)的参数为 Λ = (π, A, µ, σ),其中 π 和 A 分别对应初始概率和转移概率,µ 和 σ 是状态依赖的高斯特征分布的均值和方差(通常称为发射概率,此处用 bxt 表示)。隐马尔可夫模型的图形表示可见图 2,其中蓝色方块表示潜在变量,橙色圆圈表示观测值,绿色圆圈表示模型参数。完整似然函数可表示为:
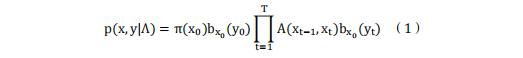
在这项工作中,一系列带有噪声的观测值是因子指数收益率,而潜在的隐藏过程则是产生这些收益率的市场状态。作者假设发射概率是高斯分布。虽然正态分布不太适合描述金融收益率,但正态分布的混合可以更好地拟合,捕捉到包括肥尾和偏度在内的典型行为(Nystrup 等人,2015;Ang & Timmermann,2012)。
隐马尔可夫模型(HMMs)的训练是通过 Baum-Welch 算法完成的,这是一种期望最大化(EM)算法(Rabiner,1989)。E 步计算给定数据和当前模型参数下,状态的对数似然期望;M 步则最大化前一步计算出的期望,以更新模型参数。算法在这两个步骤之间迭代,直到收敛。完整对数似然函数的期望由下式给出:
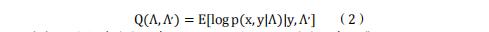
其中 Λ 是当前迭代的参数,而 Λ0 是上一次迭代的参数集。
遵循Adams等人(2016)的方法,作者对参数设置先验,并计算最大后验(MAP)估计,因此 Q 函数通过添加模型参数 Λ 的先验 G(Λ)进行修改:

EM 算法如下:在 E 步中计算第 2 步中的 Q 函数,在 M 步中最大化第 3 步中的方程。
3.2 FSHMM
特征显著性隐马尔可夫模型认为,如果一个特征的分布依赖于潜在状态,则该特征是相关的;如果其分布与状态无关,则该特征是不相关的。给定一组二元变量{z1, ..., zL}来表示特征的相关性,即当第 l 个特征相关时,zl = 1;当第 l 个特征不相关时,zl = 0。特征显著性 ρl 定义为第 l 个特征相关的概率。假设在给定状态的情况下,特征是条件独立的,这使得多元高斯分布可以写成多个一元高斯分布的乘积。因此,给定 z 和 x 的条件下,yt 的分布可以写成如下形式:

如果将这个公式的分子和分其中,r(ylt|μil, σil2)是第 l 个特征的高斯条件特征分布,而 q(ylt|ϵl, τl2)是与状态无关的特征分布。FSHMM 模型的参数为 Λ=(π,A,μ,σ,ρ,ϵ,τ),其中前四个参数对应于常规的 HMM,ρ 是特征显著性,而 ϵ 和 τ 分别是与状态无关的高斯特征分布的均值和方差。图 3 展示了特征显著性隐马尔可夫模型。
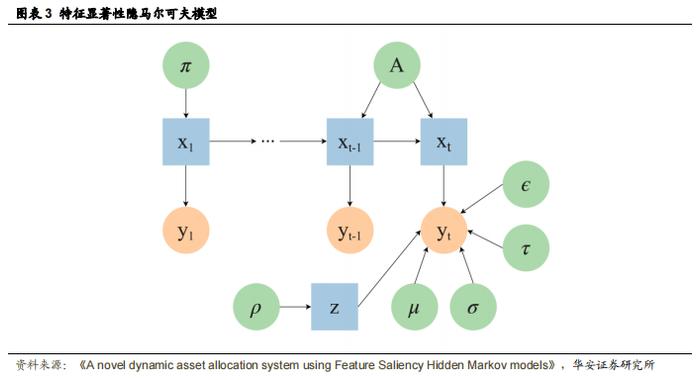

除了通过 EM 算法估计的参数外,该模型还有几个需要提前设置的超参数。其中最重要的是权重参数 kl,它可以作为 ρ 上的信息性指数先验。为参数设置较高的 kl 值会增加算法的成本,因此,为了让算法选择该特征,需要更多的证据表明该特征是相关的。这既可以用来减少所选特征的数量,也可以作为优化过程中选择特征的成本的代理。选择合理 kl值的启发式方法是将其与观测数量 T 成比例缩放,即 T/4。
3.3 Smart Beta 投资
如前所述,smart beta 是一种系统化、低成本的因子投资实现方式,其中证券的选择基于它们在过去持续获得较高回报的属性,这种属性被称为因子。因子可以是经济的根本特征(宏观经济因子)或公司的特征(风格因子)。宏观经济因子可以被视为捕捉跨资产类别的广泛风险和回报,而风格因子则可以被视为旨在解释资产类别内证券的回报和风险。
本文研究股票市场中的风格因子。在风格因子中,已经确定了数十个指标。其中大多数可以归类为族,族内的风格因子衡量相似的特征,并且通常高度相关。这方面的一个例子是动量,它包括衡量不同期间(3 个月、6 个月、12 个月等)回报的因子。虽然每个家族所属的因子没有普遍的定义,但有一些共同的主题。通常,家族包括:价值、成长、动量、质量、规模和某种形式的波动率/风险/beta 度量。这方面可能有所变化,例如,股息率有时被视为一个独立的因子家族,有时又被视为价值的一员;有时价值又可以细分为价值和深度价值。
4
数据
以下是所使用的两个数据集的描述,表 4 总结了它们的主要特征。
1.标普 500 指数每日因子数据
第一个数据集是一组基于标普 500 美国股票池构建的风格因子。首先确定每只个股的风格因子,然后对整个股票池进行排名,并构建一个投资组合,该组合包含排名前 20%的股票,并对排名后 20%的股票做空(负权重)。此过程每月重复一次。由此产生的风格因子投资组合将对因子有很高的敞口,而对整体市场没有敞口(因为负持仓抵消了正权重),表 5 展示了这些内容。该数据由一家经纪公司提供,包含 25 个风格因子,时间跨度为 1988 年至 2016 年。整个分析过程都使用了此数据集。
2.每日 MSCI 美国增强指数
第二个数据集由 MSCI 提供,包含他们发布的一系列指数。与第一个数据集一样,单个风格因子是使用基础股票及其风格因子敞口计算得出的。然后,这些单个风格因子指数被划分为六个风格因子家族,而本文正是使用了这些指数。作者使用了六个 MSCI 美国增强风格指数,即:价值、低市值、动量、质量、低波动率和股息率(Bender 等人,2013)。这些指数的起始日期不同,最近的始于 1999 年,这限制了作者使用此数据集的时间范围为 1999 年至 2016 年。
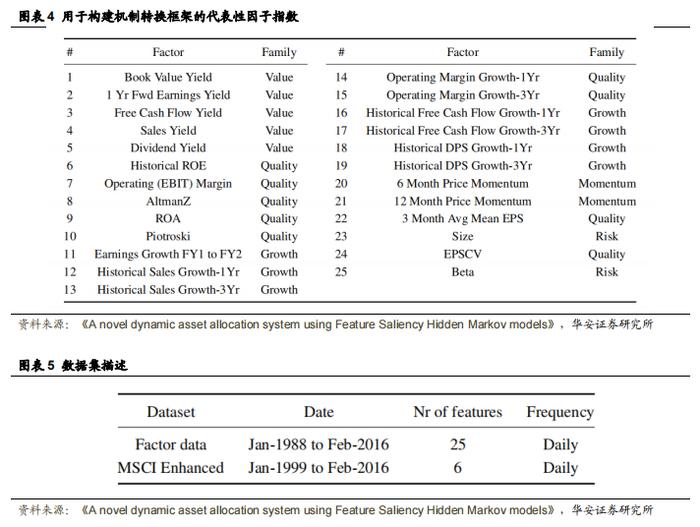
使用已发布的指数集(如 MSCI 指数)的优势在于,它们可以被另一家投资公司打包成易于投资的产品,如交易所交易基金(ETF)。例如,想要投资美国价值型股票的投资者可以购买 MSCI 美国增强价值 ETF,这样只需买入一种证券(即 ETF),而无需买入基础股票。由于无需分析和购买基础公司股票,因此可以降低实施 smart beta 策略的复杂性和成本。这使作者能够用实际资产测试作者的新型动态资产配置(DAA)系统。
5
动态资产配置系统
投资单一因子策略长期来看已经显示出显著的回报,但如何构建多因子策略并根据市场条件灵活调整因子配置并非易事。因子指数是时间序列数据,因此,作者利用隐马尔可夫模型能够识别观测序列中的潜在机制这一特性,来构建一个动态资产配置系统。作者首先将确定用于模拟市场机制的最优隐藏状态数量,然后,为了避免因频繁再平衡而产生的过高交易成本,作者将对再平衡信号进行优化。
5.1 DAA 系统
作者设计了一个动态交易框架,如图 7 所示,该框架每天进行评估,每月进行一次重新调整。每天,都会有一个新的收益向量通过扩展窗口添加到训练集中,并由作者进行状态预测。为了避免前瞻偏差,收益数据会滞后一天。由于这种预测存在噪声,因此,作者将在投资组合重新平衡之前,确定新状态下的最佳连续天数窗口。一旦状态变化被接受,作者就会从新状态中检索均值向量和协方差矩阵,并优化投资组合权重,在重新平衡后计算交易成本。一个月后,作者将这批新数据通过扩展窗口添加到训练集中,并重新训练模型。图 8 展示了作者如何使用扩展窗口每天添加数据。虽然这不会立即改变模型参数(转移矩阵和发射分布),但随着时间的推移,它们应该会略有变化以适应新信息。因此,作者能够随时间捕捉系统动态的变化。
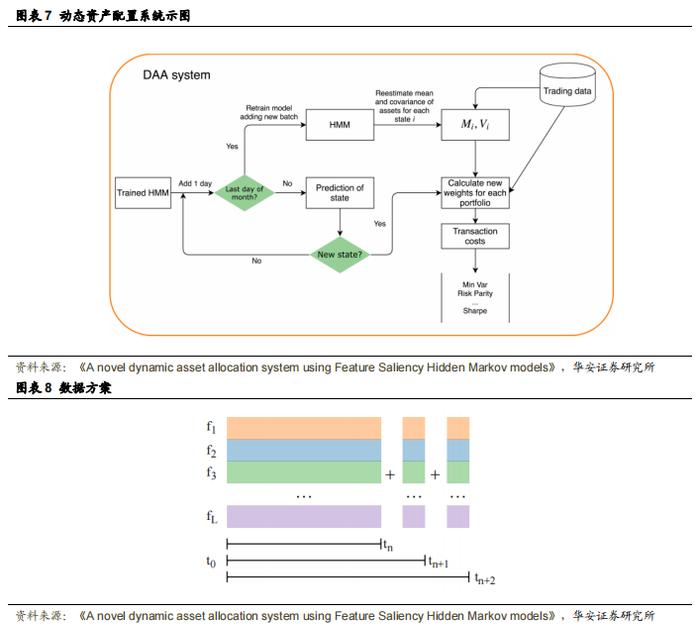
5.1.1模型选择
在训练之前,必须预先设定隐马尔可夫模型(HMM)中的隐藏状态数量。一种选择是使用贝叶斯信息准则(BIC),这是一种可用于模型选择的惩罚对数似然函数(Schwarz,1978)。BIC 的定义为:
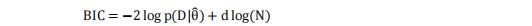
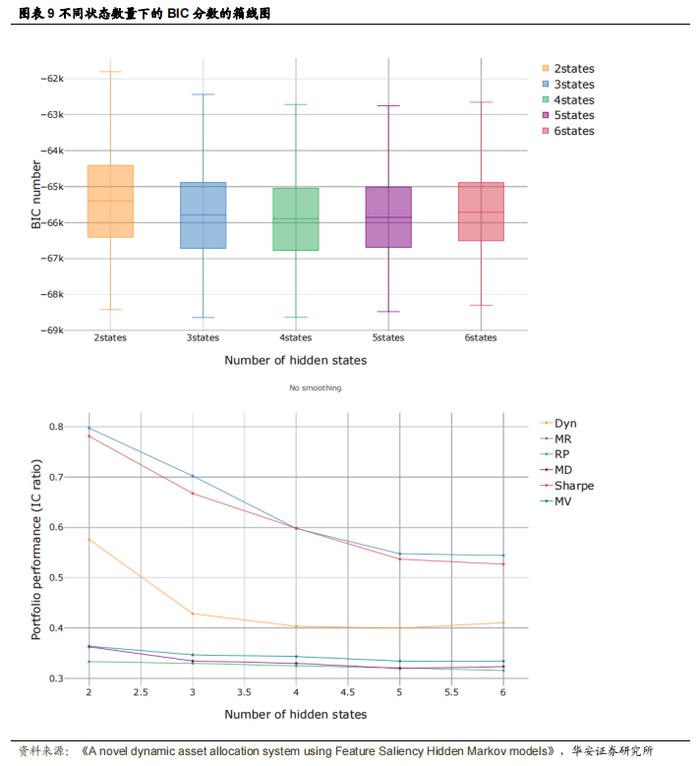
其中 d 是模型中的自由参数数量,N 是样本数量。因此,通过计算一系列 K 个状态的分数,作者可以选择分数最低的模型。另一种方法是采用贪婪策略,计算用不同数量机制构建的投资组合的表现,并选择表现最佳的模型。在金融隐马尔可夫模型文献(Guidolin & Timmermann,2008)中,机制转换模型的状态数量通常介于两个到四个之间。保持状态数量较少可以提高模型的可解释性,因此作者选择了 200 种随机组合,每种组合包含 5 种资产,并使用这些组合分别训练具有 2、3、4、5 和 6 个隐藏状态的隐马尔可夫模型。根据每个隐马尔可夫模型的信息,作者构建了不同类型的投资组合,具体将在 6.1 节中解释。每个投资组合的表现使用信息比率(年化收益率与年化波动率之比)进行计算;BIC 分数和表现随状态数量的变化如图 9 所示。对于三到六个状态,BIC 分数相当接近(四个状态时最低),而对于两个状态则略高一些。尽管这表明应使用四个状态的模型,但三个和四个状态的投资组合表现明显低于两个状态的投资组合,因此作者选择了两个状态的模型。两个状态的模型可以解释为扩张-收缩模型。
5.1.2系统校准
动态资产配置系统需要一个训练好的隐马尔可夫模型(HMM)来模拟机制变化,并选择最优的时间窗口来决定何时状态发生变化以及何时需要重新平衡投资组合。
在第一部分,作者想测试所提出的动态资产配置(DAA)系统是否能为多因子策略增值,因此作者使用多种因子组合进行测试,并为每种组合校准系统。作者从 25 个因子指数池中随机选择 n 个资产,并使用它们的收益率来训练一个隐马尔可夫模型。由于因子可以分为五个家族(见表 4),作者从每个家族中随机选择一个因子,以确保所有家族都被代表。这样总共产生了 1260 种组合。然后,作者使用相同的因子来构建投资组合。
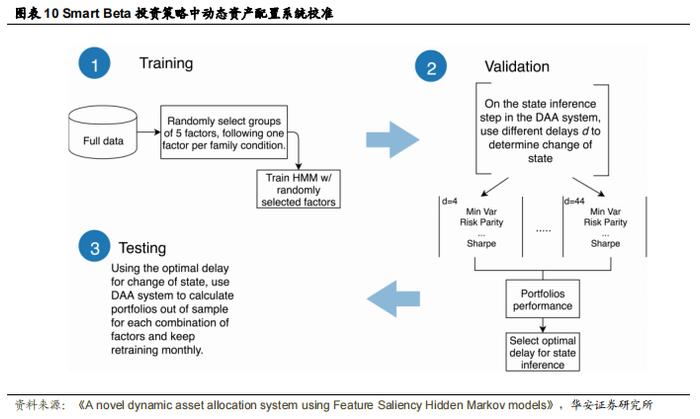
作者将数据集分为三部分:训练集(15 年)、验证集(9 年)和测试集(4 年)。为了避免陷入局部最大值,作者使用从训练数据中计算出的初始参数进行随机初始化,并选择得分最高的模型。图 10 展示了使用 DAA 系统进行训练、验证和测试的过程。
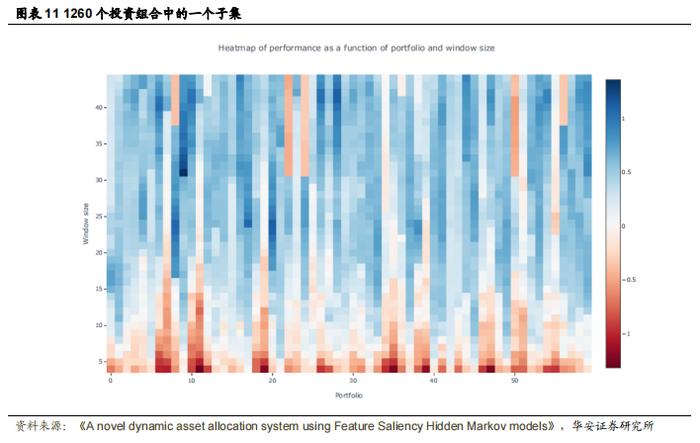
机制预测是通过传递截至前一天的整个收益率序列来解码最可能的隐藏状态序列,并将最后一个值作为状态预测。与传递整个月的收益率相比,这种每日预测更加嘈杂,作者不能每次状态变化时都重新平衡投资组合,因为这通常意味着每天都需要重新平衡。相反,在验证集中,作者寻找连续 d 天处于同一新状态的窗口,然后标记机制变化并相应地重新平衡投资组合。图 11 显示了所选投资组合的表现随时间窗口 d 的变化。虽然某些资产组合在较大的窗口下表现始终优于其他组合,但在所有情况下,较小的窗口表现最差。主要原因是投资组合的表现考虑了交易成本,因此较小的窗口意味着较高的投资组合周转率,从而导致较高的成本。作者使用训练集来确定每种资产组合的最优窗口。
5.2 具有特征显著性的 DAA 系统:FS-DAA
目前为止,作者提出的动态资产配置(DAA)系统需要提前知道用于训练隐马尔可夫模型(HMM)的时间序列特征,这可能存在限制。因此,作者提出了一种新的 DAA 系统,该系统在训练过程中融入了一种嵌入式特征选择方法,即使用第 3.2 节中描述的特征显著性隐马尔可夫模型(FSHMM)。这种方法能够选择那些有助于识别市场机制的特征,作者称之为机制依赖特征,并排除那些不依赖于市场机制的特征。
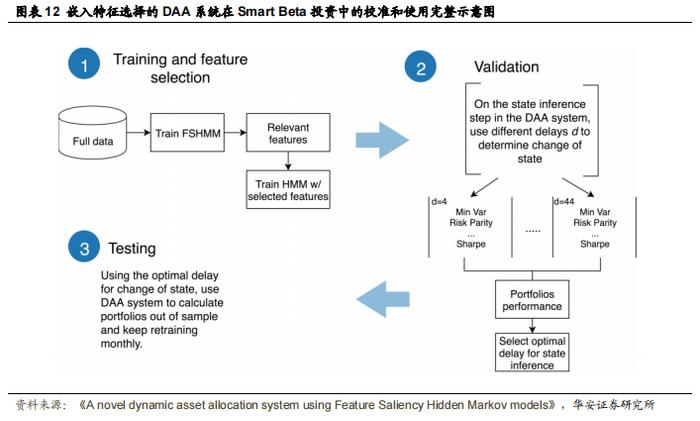
图 12 展示了使用这种新的 DAA 系统(作者称之为 FS-DAA)进行训练、验证和测试的不同阶段。FS-DAA 接收多个时间序列数据,并拟合一个 FSHMM,该模型为每个时间序列分配一个显著性值。显著性值越高,意味着该特征越重要,被选中的可能性越大。由于 FSHMM 假设特征是条件独立的,因此拟合的模型具有对角协方差矩阵。作者选择了这些重要的特征,并使用它们来训练一个具有完整协方差矩阵的 HMM。
为了评估 FSHMM 是否能够区分相关特征和噪声,作者首先生成了一些无关的随机噪声特征,并将它们添加到作者的每日因子数据集中。作者使用不同数量的特征、观测值和 kl 值进行了测试。对于每种情况,所有特征(包括相关特征和噪声特征)的 kl 值都是相同的。测试结果汇总在表 A.5 和 A.6 中。在所有情况下,算法都为无关特征分配了较低的显著性值,而为相关特征分配了较高的显著性值。
接下来,作者使用因子数据集中的所有 25 个特征训练了一个 DAA 系统,并训练了一个 FS-DAA 系统。FS-DAA 系统接收这 25 个特征,选择其中重要的特征,然后仅使用这些因子训练一个 HMM,并比较所获得的机制。最后,作者使用这两个系统构建了一个使用 MSCI 美国增强型因子指数系列的投资策略。两个模型都使用 16 年的数据(从 1990 年到 2006 年)进行训练,然后每月重新训练,直到 2016 年。作者使用 7.5 年的交易数据(从 1999 年 1 月到 2006 年 6 月)来估计每个机制下 MSCI 指数的均值和协方差,以便对两个机制的协方差矩阵进行稳健估计。然后,作者使用 6 年的验证集来选择最佳的时间窗口来设置状态变化,并使用 4 年的测试集进行测试。
所提出的 DAA 系统的一个优点是,它允许作者将用于训练 HMM 以检测机制的数据与用于资产配置的数据分开。这对于因子投资非常有用,因为作者可以构建具有长期历史的因子(如因子数据集),然后使用具有较短历史的实际可投资资产(MSCI 增强型数据)来构建投资组合。
6
结果及分析
首先,作者将 DAA 系统的表现与大型因子数据集上的基线策略进行了比较。然后,讨论了 FSHMM 算法的实现。最后,作者使用 MSCI 指数数据集对提出的 FS-DAA 系统进行了实际资产测试。
6.1 交易策略和基准
作者并没有只构建一种投资组合,而是构建了多种:风险平价、最大分散化、最小方差、最大收益、最大夏普比率以及一种改进的最大收益。风险平价(RP)、最大分散化(MD)和最小方差(MV)的构建仅考虑了协方差矩阵,因此它们可以被认为更具风险意识。最大收益(MR)、最大夏普比率(Sharpe)和改进的最大收益(Dyn)在构建过程中都考虑了收益的均值,因此它们往往更激进。为了进行比较,作者还构建了一个等权重投资组合以及每种资产组合的基准。每个基准都使用与其对应的 DAA 系统相同的优化方法进行构建,但每月进行一次再平衡,并且使用“单一区制”的历史收益来估计协方差矩阵。而 DAA 系统则有两个协方差矩阵,每个机制一个。所有投资组合及其基准的构建都考虑了交易成本。交易成本是通过将投资组合周转率(即投资组合的再平衡程度)与每次买卖 50 个基点(0.5%)的交易成本相乘来计算的。
6.2 DAA 系统与基线策略的比较
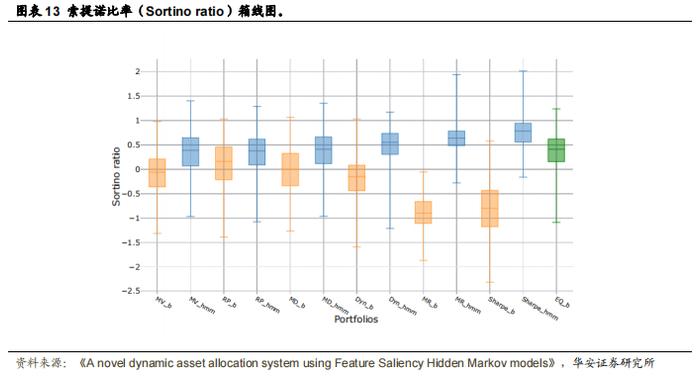
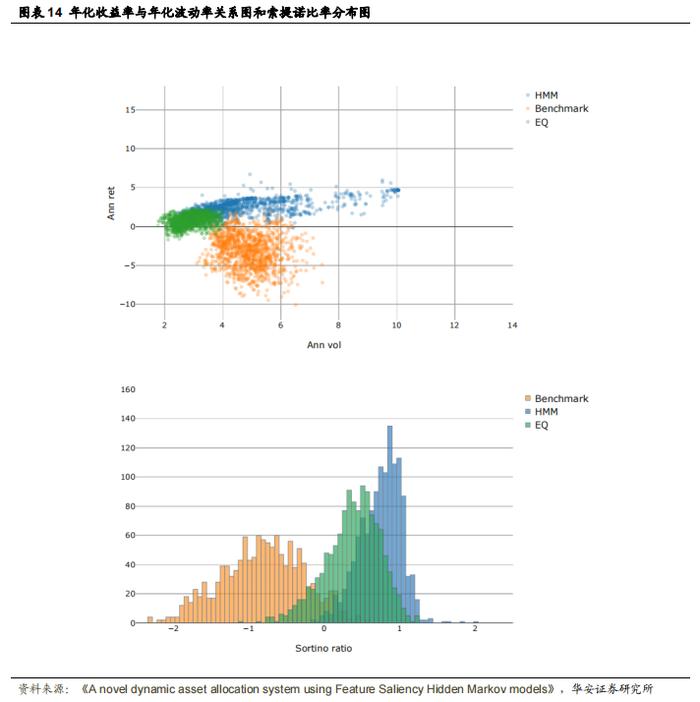
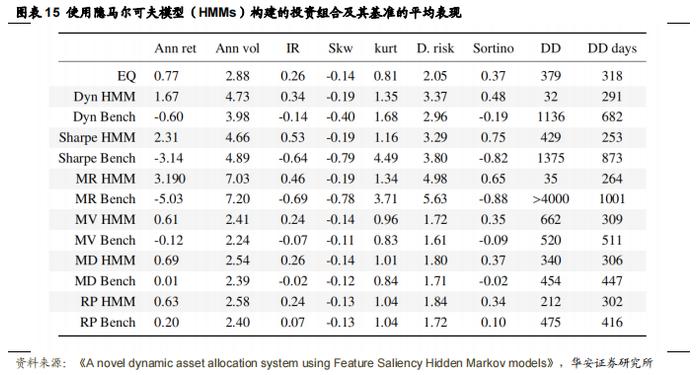
作者首先使用 1260 种随机选择的资产组合来训练隐马尔可夫模型(HMM)并进行资产配置,以此评估 DAA 系统,并将其与基准进行比较。图 13 展示了使用 DAA 系统计算的所有投资组合以及它们的基准的索提诺比率(Sortino ratio)表现。可以看出,使用机制信息构建的所有投资组合的表现都优于其对应的基准。由于在计算过程中使用了平均收益,因此更注重收益的投资组合相对于其基准有显著提升,而更注重风险的投资组合相对于其单一机制对应的投资组合有所改善,但与等权重投资组合的表现相似。表现最好的投资组合是夏普比率(Sharpe)投资组合,它在构建过程中同时考虑了均值和协方差。图 14-上部分展示了夏普比率投资组合及其基准的年化收益率与年化波动率的关系。使用 HMM 构建的投资组合的无条件收益率高于其对应的基准,且收益率和波动率均高于等权重(EQ)投资组合。图 14-下部分展示了相同投资组合的风险调整后收益指标(索提诺比率)。可以看出,HMM 投资组合的表现优于其基准。表 15 展示了每种类型投资组合的平均表现指标。在大多数情况下,HMM 投资组合在所有指标上的表现都优于其无条件基准,且更注重收益的投资组合的表现优于等权重投资组合。注重收益的投资组合的表现提升来自于更高的收益率和风险降低。此外,在大多数情况下,偏度和峰度均低于基准收益率,且最大回撤更低(且持续时间更短)。
6.3 基于因子隐马尔可夫模型(FSHMM)的动态资产配置(DAA)系统
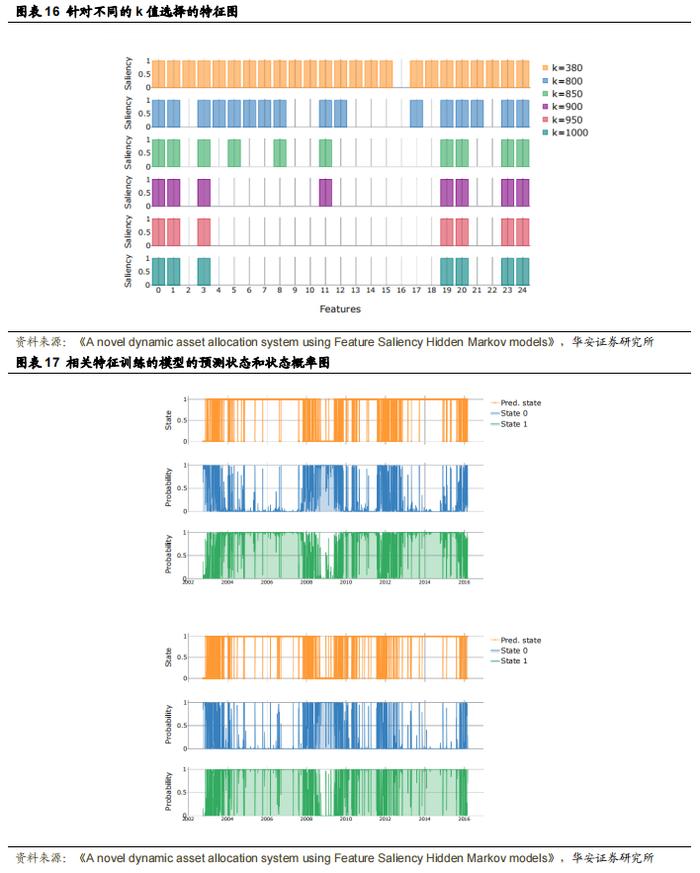
作者随后使用该算法在包含 25 个因子指数的数据集中检测相关特征。图 16 展示了不同 k 值下所有因子收益序列的特征显著性。由于训练集包含约 3800 个观测值,作者根据 Adams 等人(2016)提出的启发式方法,选择了接近该数量四分之一的 k 值。所选特征包括:账面价值收益率、1 年期预期收益收益率、销售回报率、6 个月价格动量、12 个月价格动量、每股收益变化(EPSCV)和贝塔系数(Beta)。这些特征很有意思,因为它们代表了第 3.3 节中提到的六或七个因子家族中的四个。为了进行比较,作者使用全部 25 个特征训练了一个隐马尔可夫模型(HMM),并使用所选资产训练了另一个模型。图 17 展示了模型训练后的预测状态和估计概率。作者将状态 1 识别为“良好状态”,将状态 0 识别为“不良状态”。图表清晰地识别出了 2008 年的经济危机——其初步迹象于 2007 年 8 月和 9 月开始显现,2008 年 1 月至 5 月间出现了一些波动,然后在 2008 年 9 月爆发了严重的崩溃。两个模型都识别出 2007 年下半年状态 0 的激增,并在 2008 年期间完全转变为状态 0。使用相关特征训练的模型对困境状态更为敏感——它处于此状态的时间占比为 24%,而使用全部特征训练的模型处于此状态的时间占比为 20%。状态 0 的平均持续时间为 3.8 天,而完整模型的平均持续时间为 3.2 天。在计算这些值时,未对预测概率进行平滑处理。
6.4 基于 MSCI 指数的动态资产配置-特征选择系统
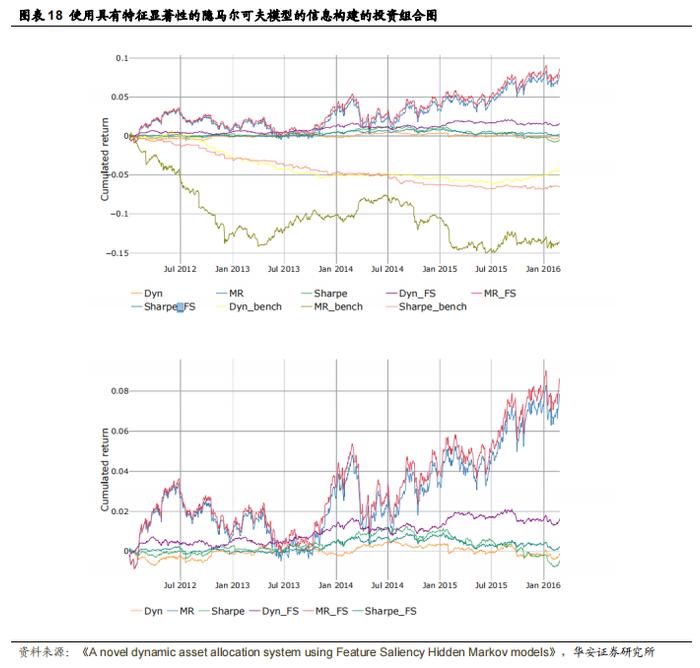
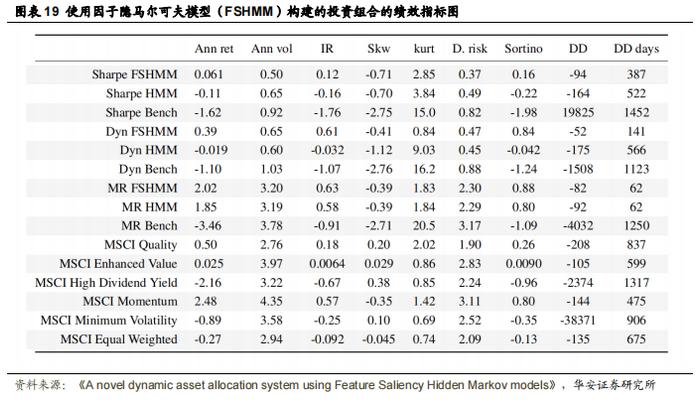
在本节中,作者使用每日因子数据集中经过特征选择后的因子子集以及 MSCI 增强因子进行资产配置,评估了动态资产配置-特征选择(DAA-FS)系统的表现,并将其与未进行特征选择的 DAA 系统进行了比较,后者使用数据集中的全部 25 个因子训练隐马尔可夫模型(HMM)。为简化起见,作者仅计算了 Sharpe、MR 和 Dyn 投资组合,因为在构建过程中使用状态转换模型时,它们的表现明显优于风险聚焦投资组合及其基准。图 18 展示了这三个投资组合在使用完整特征 HMM、因子隐马尔可夫模型(FSHMM)以及未使用状态信息构建的基准的累积收益率。两个 HMM 投资组合的表现均优于其基准(上图),而使用特征选择构建的 HMM 投资组合的表现略优于使用完整特征 HMM 构建的投资组合(下图)。表 19 展示了所有投资组合和 MSCI 增强指数(扣除市场因素)的绩效指标。所有指标均为年化指标,且为样本外数据,涵盖 2012 年 1 月至 2016 年 2 月期间。使用 DAA 和 FSDAA 获得的结果显示,与基准相比,它们的表现有了显著的提升。可以看出,在此期间,仅有三个 MSCI 指数的信息比率(IR)为正,而在所有情况下,两个 FSHMM 投资组合的信息比率均为最高。与基准和 MSCI 指数相比,使用完整特征 HMM 或 FSHMM 的大多数情况下都实现了下行风险的降低。
7
结论和未来展望
本文的主要研究重点是通过使用状态转换模型来改进 smart beta 策略。本文的主要贡献如下:
作者已经证明,使用经过与将用于资产配置的相同资产训练的、具有两个潜在状态的隐马尔可夫模型(HMM)的信息来构建投资组合,可以改善投资组合表现。作者通过计算不同类型的投资组合(从更注重风险的投资组合到更具侵略性的投资组合)对此进行了测试。对于收益导向型和平衡型投资组合(其中收益或风险调整后的收益得到优化,平均每年超过市场的信息比率达到 50%),这种改进更为显著;而在更注重风险的投资组合(如风险平价、最小方差和最大分散化)中,这种改进则不太明显,平均每年的信息比率仅提高了 25%。
作者开发了一个系统性的资产配置框架,该框架使用嵌入式特征选择算法来识别与模型相关的特征。这提高了模型的准确性,并使投资组合构建方法更加客观,因为它有助于防止特征选择过程中的偏差。作者使用因子隐马尔可夫模型(FSHMM)算法从一组众所周知的因子指数中选择相关特征,并将其与使用全部资产训练的 HMM 进行了比较。两个模型在状态识别上均表现出一致性,而仅使用相关特征训练的模型对经济困境时期的敏感度更高。
作者通过 MSCI 美国增强因子指数,使用真实、可投资的资产对两个模型进行了测试。与使用全部特征训练的 HMM 相比,使用经过相关特征训练的 FSHMM 的信息构建的投资组合表现更好。
未来研究的模型扩展可能包括在 HMM 中纳入宏观经济序列,其中嵌入式特征选择可能有助于解决选择相关经济序列的问题,从而更准确地识别经济周期。这对于其他资产类别(如固定收益)尤其有趣,但这不在本文的讨论范围内。
使用 HMM 的一个缺点是潜在状态的数量必须提前已知,或者通过贝叶斯信息准则(BIC)选择,这并不总是有效的,或者通过贪婪方法选择表现更好的模型。这可以通过使用无限 HMM(Beal 等人,2002)来解决。
“
文献来源
核心内容摘选自 Elizabeth Fonsa,, Paula Dawson , Jeffrey Yaua, Xiao-jun Zeng , John Keane 于 2021 年 1 月在《Expert Systems with Applications》上发表的论文《A novel dynamic asset allocation system using Feature Saliency Hidden Markov models》。
文献结论基于历史数据与海外文献进行总结;不构成任何投资建议。
本报告摘自华安证券2024年8月28日已发布的《【华安证券·金融工程】专题报告:基于特征显著性隐马尔可夫模型的动态资产配置》具体分析内容请详见报告。若因对报告的摘编等产生歧义,应以报告发布当日的完整内容为准。
分析师:严佳炜 执业证书号:S0010520070001
分析师:吴正宇 执业证书号:S0010522090001


