来源:华泰金融工程
林晓明 S0570516010001 研究员
李 聪 S0570519080001 研究员
韩 晳 S0570118090078 研究员
王佳星 S0570119090074 联系人
报告发布时间:2020年10月27日
摘要
本文基于真实数据实证了不同条件协方差估计方法的表现
均值-方差投资组合理论中,协方差矩阵是衡量投资风险的统计量,在量化投资中有广泛应用,其估计的精确与否直接影响模型的最终表现。考虑到金融数据具有时变性,本文研究了基于指数移动平均与多元GARCH模型的条件协方差估计方法。主要内容包括:1、综述条件协方差估计方法中两类协方差估计模型的原理;2、给出统一的评价体系,保证条件协方差估计方法实证结果的可比性;3、基于国内外七类资产组合的真实交易数据验证条件协方差估计方法相比于样本协方差的改善程度;4、总结分析各算法的优劣,并针对不同配置场景提供实操建议。
指数移动平均反映近期变化趋势,多元GARCH 模型反映均值回复特征
考虑到金融市场的时变性,资产的波动率和相关性往往会呈现出时变规律,久远的历史样本很可能无法反映现状,这与无条件协方差矩阵不随时间变化的假设相矛盾。因此,本文重点针对这个问题引入条件协方差估计方法作为解决方案。其中,基于指数加权移动平均法的Riskmetrics模型和Barra半衰期模型考虑到近期观察值更能反映近期变化趋势,对近期的样本赋予更多的权重;而多元GARCH模型不仅考虑了资产收益率的波动率聚集现象,同时在模型设定中考虑了长期均值回复的效应。两类估计方法都能捕捉收益率的时变特征,理论上都会改进无条件协方差矩阵的估计。
评价指标:最低波动组合与目标波动组合的样本外表现
本文选取国内股票、行业、大类资产和全球股、债、商品等大类资产2007年以来的真实数据,针对每种条件协方差估计方法,分别构建最低波动组合与目标波动组合,考察样本外的波动率表现。具体地,本文在每月末基于指定窗宽的历史数据计算各类协方差估计量,进而求解两类组合对应的权重,评估在回测区间内,年化波动率是否相对于使用样本协方差有所改善。理论上,协方差估计越精确,则构建的最小波动(或目标波动)组合的波动水平就应该越小(或越接近目标水平)。
条件协方差对于最小波动组合更为适用且Barra 半衰期模型适用性最广
实证结果表示,条件协方差估计更适合于构建最小波动组合,其中,Barra模型能够在大部分资产组合场景下有效改善估计的时效性和精度,Riskmetrics模型仅在少部分场景下适用,而多元GARCH模型更适合对海外资产进行建模。压缩估计类算法更适用于构建目标波动组合,虽然部分样本协方差方法对于原始组合亦有不同程度改进,但总体而言改善效果不及压缩估计模型。这可能是由于模型本身消除历史信息无效性的需求较低所导致的。
风险提示:模型根据历史规律总结,历史规律可能失效。报告中涉及到的具体资产、股票不代表任何投资意见,请投资者谨慎、理性地看待。
报告正文
本文研究导读
在前期研报《不同协方差估计方法对比分析》(2019-11-5)中,我们提出获得最优的协方差矩阵估计方法需要解决两个问题:样本长度不足导致的估计误差;久远历史样本反映现状的无效性。
针对第一个问题,上篇研报给出了样本不足时样本协方差矩阵的缺陷并提出相应的解决办法。在样本数量不足的情况下,POET模型和压缩估计模型的估计误差比样本协方差矩阵小,可以作为样本数量不足时协方差矩阵估计的解决方案。
相比于使用复杂的协方差矩阵估计方法,增加样本长度显然是解决协方差估计误差更简单的做法。然而,金融数据具有时序性,久远的历史样本很可能无法反映现状,这就涉及到协方差估计的第二个问题,即久远样本反映现状的无效性。本文重点针对上述第二个问题,引入条件协方差估计方法作为解决方案。
根据估计对象的不同,协方差矩阵估计方法可以分为无条件协方差估计和条件协方差估计两大类。前者假设协方差矩阵不随时间变化,即每期观测变量之间是独立同分布的;后者则假设𝑡时刻的协方差矩阵与𝑡时刻之前的协方差矩阵有关。本文主要介绍指数加权移动平均模型和多元GRACH模型两类条件协方差估计方法,在实证分析中,将无条件协方差估计方法中的样本协方差方法作为基准,压缩估计作为对照,比较分析了RM1996、RM2006、USE4S、USE4L、CCC、DCC等条件协方差估计方法在最低波动组合的样本外表现、目标波动组合的表现。
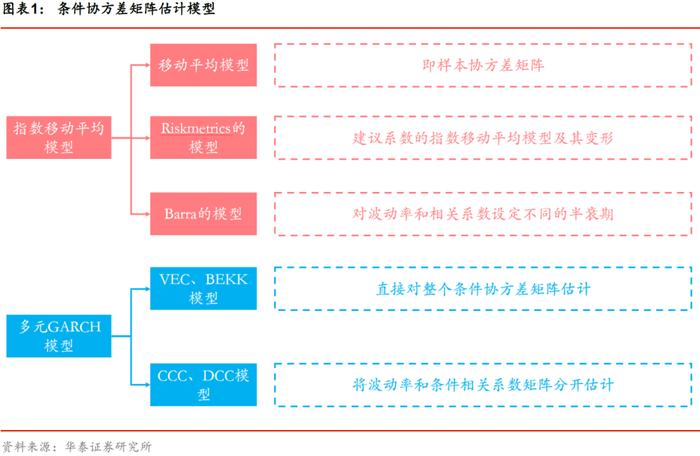
本篇报告后续内容安排如下:第二部分将综述主流的条件协方差估计方法中的指数移动加权平均模型以及多元GARCH模型,第三部分将给出条件协方差估计方法的评价体系,第四部分将实证不同条件协方差估计方法在不同场景下的表现,最后一部分将总结分析各算法的优劣及在不同场景下的适用性。
条件协方差估计方法介绍
基准:普通移动平均协方差(无条件协方差)
移动平均协方差(Moving Average Covariance)是最简单的条件协方差估计量,其计算公式如下。
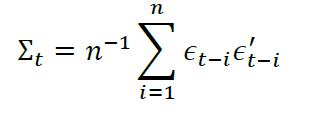
其中,Σt为第t期的协方差矩阵,为未知量,待估计;εt-i是第t-i期资产收益率的零均值残差向量,为已知历史信息。由上式可知移动平均协方差是集合{εt-iεt-i'}中每个元素的等权平均,即,对历史各个时间点的元素赋予相同的权重。
然而,金融时间序列数据往往是时变的,例如在金融危机时资产间的相关性会明显地增大,资产收益率的波动也更加剧烈,久远的历史数据样本不能反映近期的信息,应该赋予较小的权重。相对来说,移动平均协方差对近期和远期的样本等权平均,不能准确估计协方差矩阵,对不同时刻的样本赋予不同的权重可能是更合理的做法。
移动平均协方差是一类典型的无条件协方差估计方法,我们引入条件协方差作为改进。条件协方差考虑了序列的时变性,将多元收益率rt表示为
rt = μt + εt
其中μt = E(rt|Ft-1)是rt在给定过去信息Ft-1下的条件期望,εt是第t期资产收益率的零均值残差向量。条件协方差可以表示为
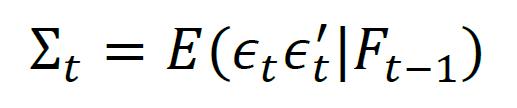
从公式可以看出,条件协方差和无条件协方差的区别在于增加了过去信息作为已知条件,这也更符合真实的金融建模场景。
指数加权移动平均协方差
指数加权移动平均协方差(Exponentially Weighted Moving Average Covariance)是一种典型的条件协方差估计方法,该方法考虑到近期观察值更能反映近期变化趋势,对预测值有较大影响,因此对近期的样本赋予更多的权重,计算条件协方差矩阵的公式如下:
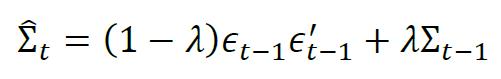
其中λ∈(0,1),当t足够大时,上式与如下表达式近似
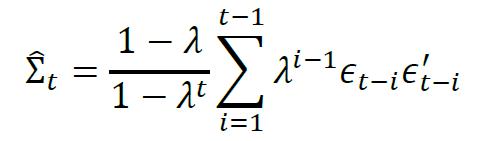
从公式中可以看出,指数加权移动平均方法对于历史信息赋予λi-1的权重,λ是一个小于1的正数,离当前时间点的距离越大,则权重越小。本质上是将历史信息的权重随时间衰减。实际应用中通常的取值接近于1,下文将介绍几个经典的指数移动加权平均协方差模型。
RiskMetrics1996模型
RiskMetrics模型是J.P.Morgan在开发在险价值(VaR)建模时提出的协方差估计方法,在1996年由J.P.Morgan和路透社向公众推出。RiskMetrics模型与上述典型指数加权移动平均模型有相同的协方差计算公式,即
RiskMetrics模型直接指定了λ的数值,对于日度数据λ取0.94,月度数据λ取0.99。
RiskMetrics2006模型
RiskMetrics模型的优势在于其原理和计算上的简单性,通常用于估计日度、月度数据的条件协方差。然而,由于不同频率的序列包含的样本信息量不同,每次估计条件协方差时,权重λ需要针对序列频率修改,从而对所得估计量进行尺度修正。比如,日度数据中λ取0.94,月度数据取0.99,但对于年度数据,甚至更低频率的序列,模型没有给出λ的参考取值,这就导致了RiskMetrics模型使用的局限性。此外,RiskMetrics模型采用指数加权移动平均法直接计算协方差,对时间序列本身缺乏统一的理论模型刻画,难以得到较好的统计性质。因此,RiskMetrics2006模型对RiskMetrics模型进行了拓展,增加了对资产收益的时间序列建模估计,修改了估计方程的形式,使得参数无需针对样本频率修改,能够更好地适用于不同频率的时间序列条件协方差估计。针对λ需要频繁根据序列频率修改的问题,RiskMetrics2006模型采用人为设定的时间间隔τi,进行采样,仍然使用指数加权移动平均模型计算相应资产收益率序列的条件协方差,其中的权重系数λi由时间间隔τi,再对不同频率采样所得的协方差估计量加权平均,得到最终估计结果。
本质上,RiskMetrics2006模型是在不断增长的时间范围内,对多个不同频率时间序列RiskMetrics模型的再次加权平均。这样解决了RiskMetrics模型只适用于短时间、高频率序列的问题,能够完成市场上不同时间维度的序列预测。
单一频率下条件协方差的估计与RiskMetrics1996类似,其具体计算公式如下
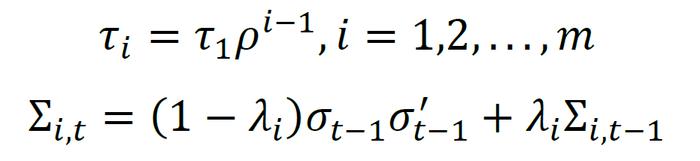
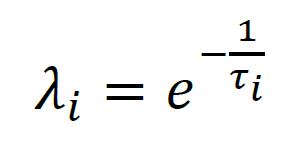
其中,σt-1是第t-1期的资产收益率残差标准差,{τi}是人为设定的采样时间间隔序列,由ρ,τ1,τmax决定。是用来确定时间间隔的衰减系数,它的取值在1附近,不会对估计结果有显著的影响,通常取ρ=
接下来,用对数衰减系数ωi,对不同时间间隔τi,即不同频率下的条件协方差估计量加权平均,以消除RiskMetrics1996模型中参数对序列频率的依赖性。
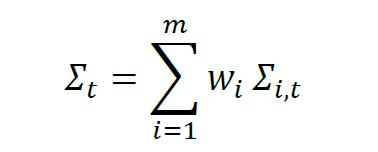
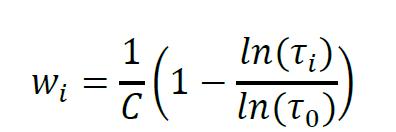
其中,C是一个使得
从样本权重随时间的变化上看,RiskMetrics1996模型的权重呈指数衰减,而RiskMetrics2006模型的权重呈双曲线衰减,下图展示了120个样本的权重变化
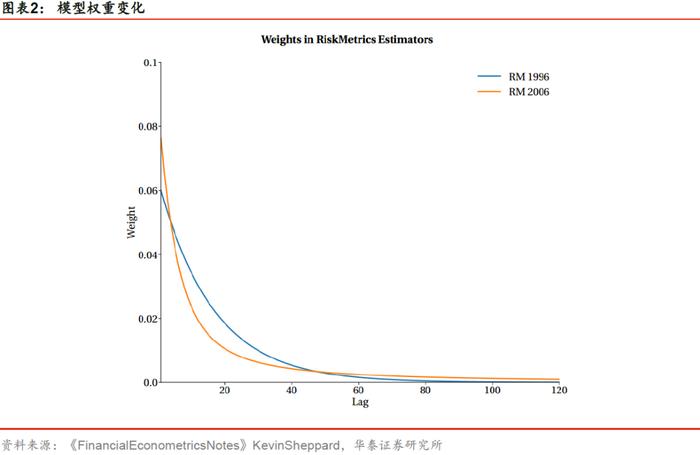
两个模型的原理不同,衰减速度也有差异。计算可得,在日度数据的RiskMetrics1996模型中,前75个观察值占据了99%的权重,而RiskMetrics2006模型需619个观察值才占比99%的权重。结合上图,我们发现RiskMetrics2006模型相比RiskMetrics1996模型,对近期数据赋予的权重更小,对历史久远的数据赋予的权重更大。
Barra半衰期模型(USE4L,USE4S)
Barra的风险模型也有应用指数加权移动平均的方法。本部分将介绍Barra半衰期模型中对条件协方差矩阵的两个经典估计模型:USE4S和USE4L。二者具有完全相同的原理,但模型中具体的参数取值有所不同。USE4S模型更适用于高频数据的协方差估计,USE4L模型则主要针对低频数据的协方差估计。
在高维情况下估计条件协方差矩阵时,常见的问题是历史数据不足,矩阵不稳定,误差较大。因此,与RiskMetrics系列模型直接估计条件协方差矩阵不同,Barra半衰期模型将方差和相关系数矩阵分开估计,进而得到条件协方差矩阵。其中,方差直接用指数加权移动平均法估计,相关系数矩阵根据指数加权移动平均法估计所得的协方差矩阵,通过其对角线上的方差归一化后得到。对方差和相关系数分开估计,使其中的半衰期和权重参数能根据二者不同的误差原因灵活调整。更有利于提高协方差矩阵估计的精度。
模型首先对方差进行估计,使用指数加权移动平均法,其具体计算公式如下
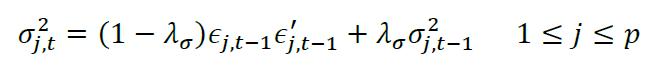
其中ρ代表资产数量,对p个资产的方差分别估计,σj,t2是第j个资产第t期方差的估计,εj,t-1是第j个资产第t-1期资产收益率的零均值残差向量,τσ是方差估计模型的半衰期。权重
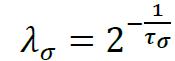
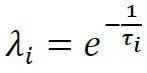
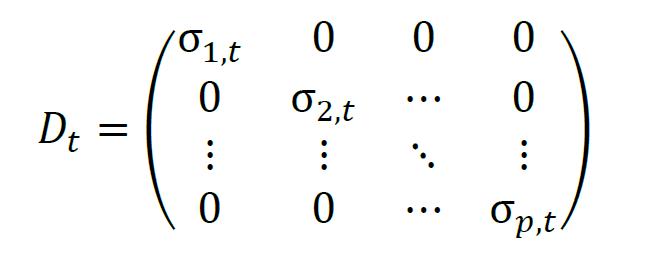
接着,模型同样利用指数加权移动平均法,先计算协方差矩阵,再用方差归一化后得到相关系数矩阵,其具体计算公式如下:
其中,Qt是t时刻的协方差矩阵,εt-1是第t-1期资产收益率的零均值残差向量,
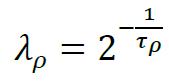
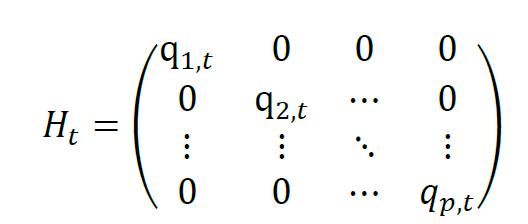
因此,将协方差矩阵Qt利用标准差矩阵Ht归一化之后得到相关系数矩阵Rt
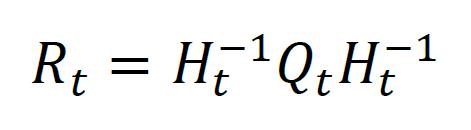
最后,根据条件协方差的计算公式,由标准差构成的对角阵Dt和相关系数矩阵Rt,得到t时刻的条件协方差矩阵Σt为
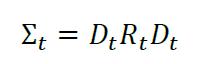
两个模型中,方差半衰期应比相关系数矩阵的半衰期短。因为同一资产的波动水平在不同时间段内基本处于同一量级,方差作为对角元素对条件协方差矩阵估计结果的影响较小;但不同资产间的相关系数可能相差很大,因此易使最终结果产生较大的估计误差,需要使用较长的半衰期,即纳入更多的历史数据进行预测。USE4模型的文档里提供了两种方差模型和相关系数模型的半衰期组合,分别是(τσ,τp) = (84,504)或者(252,504),即我们后文将要用到的USE4S和USE4L。其中,USE4S中τσ更小,说明它主要考虑了近期数据对估计的影响,对短期变动更敏感,因此更加适用于高频数据的协方差估计。总的来说,USE4S模型对于日度、月度数据的条件协方差预测更为灵敏和准确,USE4L模型专为基于稳定风险预测而进行交易的长期投资者分析年度数据而设计。
可以看到,Barra半衰期模型的核心是根据不同频率的数据选择合适的半衰期确定权重,对方差和相关系数矩阵分别估计以提高估计精度,最终得到估计误差较小的条件协方差矩阵。
多元GARCH模型
除调整历史样本权重外,提高协方差估计精度的另一个途径是对金融时间序列的建模预测。金融时间序列往往具有异方差性质,并且存在显著的波动率聚集现象,即收益率的波动率在一段时间会比较大,而另一段时间会比较小。对于资产收益rt,自回归条件异方差模型(ARCH)能有效地刻画出随时间变化的条件异方差:
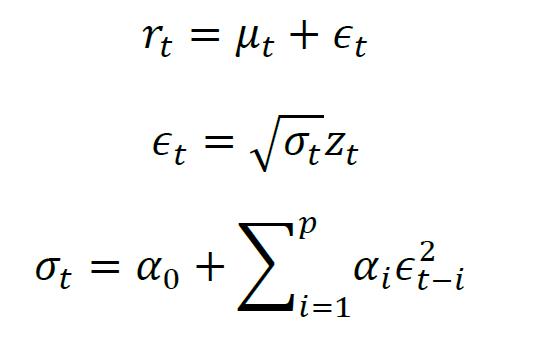
其中,rt是资产收益率,μt = E(rt|Ft-1)是rt在给定过去信息Ft-1下的条件期望,εt是第t期资产收益率的零均值残差,σt是残差的条件方差,zt是服从正态分布的均值为0、方差为1的随机变量,p是设定的滞后阶数,αi是刻画条件方差时序相关性的系数,可以由样本估计得到。根据这一模型,大的扰动εt来源于大的条件方差σt,从而影响下一期的条件方差σt+1,使下一期也继续产生大的扰动,反之亦然。因此,ARCH模型反映了金融时间序列波动率聚集的特点。
在实际操作中,由于ARCH模型的滞后阶数p难以确定,广义的ARCH模型(GARCH)更被普遍使用。同ARCH模型相比,GARCH模型的条件异方差满足下式:
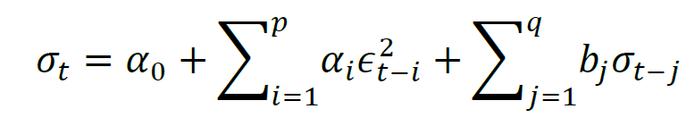
GARCH模型有两个滞后阶数:p与q。可证明,GARCH(1,1)等价于无穷阶的ARCH模型。另一方面,同指数移动加权平均协方差相比,GARCH模型也相当于对最近的样本赋予较高的权重,与当前时点距离越远,对应的权重越小。不同的是,GARCH模型估计的方差序列会逐渐衰减到α0这一项,而α0与无条件方差(即样本方差)成比例,因此,GARCH模型对条件方差的估计隐含着均值回复的性质,更适合对平稳序列建模,在实证中,我们通常会对原始时间序列做一阶差分处理,以充分利用GARCH模型的这一优势。
VEC模型
对于金融市场上的多个资产,一元的GARCH模型只能捕捉单变量的时序特征,而金融资产间关联紧密,有必要引入多元GARCH模型来刻画多个资产收益率的协方差。最早的多元GARCH模型是Bollerslev(1988)提出的VEC模型(VectorGARCHmodel),VEC模型实际上是对协方差矩阵中的每个元素建立一元GARCH模型,即一系列GARCH模型的组合。以简化版本的对角VEC模型为例,假设rt是M×1维的资产收益率向量,满足:
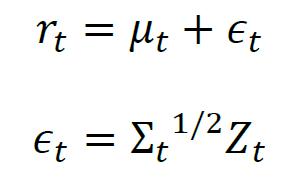
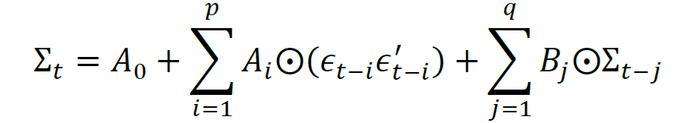
与一元GARCH模型类似,μt = E(rt|Ft-1)是rt在给定过去信息Ft-1下的条件期望向量,通常使用ARIMA模型自动选择最优的滞后阶数估计,εt是收益率减去条件均值后M×1维的残差向量,Zt服从M维正态分布,其均值向量为0,协方差矩阵为单位阵I。Σt为条件协方差矩阵,Ai,Bj是滞后项系数矩阵,
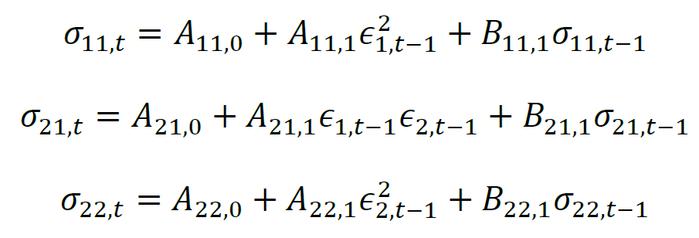
对于一般的VEC模型形式,所需估计的参数数量与M4成比例,在有多个金融资产的情形下,估计难度极高。另一方面,若不对参数施加限制,则难以保证所估计的协方差矩阵的正定性,使得协方差矩阵在实际使用中失去意义。
BEKK模型
为了减少VEC模型的参数个数,以及满足协方差矩阵的正定性性质,Baba、Engle、Kraft、Kroner(1995)提出了BEKK模型。在这一模型中,条件协方差矩阵满足:
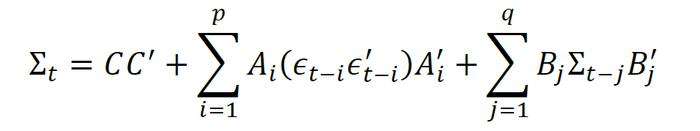
其中,C是一个M×M的下三角矩阵,Ai和Bj是M×M矩阵。由于矩阵CC'是正定的,则Σt几乎处处正定。在BEKK模型中,未知参数的总数为M2(p+q) + M(M+1)/2,相比VEC模型已大大减少,然而每当p和q增加1单位时,模型需要估计的参数仍然会迅速增长。因此,虽然BEKK模型解决了VEC模型中不能保证协方差矩阵正定性的问题,但需要估计的参数依旧繁多,并且模型中的系数Ai和Bj在实际操作中也没有直接而合理的解释。
CCC模型
VEC模型与BEKK模型都是直接对条件协方差的动态演变过程建模。Bollerslev(1990)另辟蹊径,提出了常相关多元GARCH模型(CCC),将条件协方差矩阵分解为条件方差与条件相关系数两部分,即Σt = DtRDt。其中,Dt为条件标准差
CCC模型未知参数的总数为M(p+q) + M(M+1)/2,相比BEKK模型进一步减少。然而, CCC模型将相关系数设定为常数不太符合实际,不能捕捉收益率的动态相关性。
DCC模型
Engle (2002)对CCC模型进行了改进,提出了动态相关系数模型(DCC)。与CCC模型相比,DCC模型的最大特点是假设相关系数矩阵是时变的,即
其中diag(Qt)为Qt的对角元排列而成的对角矩阵,Qt满足:
ut-1=Dt-1-1εt-1为对残差εt-1的标准化,
协方差估计方法汇总
在实证分析中,我们考虑使用样本协方差矩阵作为基准模型。在指数移动加权平均类模型中,我们考虑了经典riskmetrices模型以及改进后的riskmetrices2006模型。此外,我们还考虑了Barra的USE4文档中介绍的长期和短模型,分别记为USE4L和USE4S,USE4L模型中波动率的半衰期为252,相关系数矩阵的半衰期为504,USE4S模型中波动率的半衰期为84,相关系数矩阵的半衰期为504。
在多元GARCH类模型中,我们只考虑常相关系数矩阵模型(CCC)和动态相关系数矩阵模型(DCC)。这是因为,VEC模型在定义上就不能保证估计量的正定性,实践价值较小,而BEKK模型需要估计的参数太多,极有可能导致模型优化失败,即使是最简单的BEKK(1,1)模型,在大类资产实验场景下需要估计参数为497个,在股票投资组合实验场景下模型需要估计的参数高达6275个。CCC和DCC模型本质上是对每个资产建立一个单变量GARCH模型,再对相关系数建立一个多变量GARCH模型。尽管这两个模型的估计参数比VEC模型和BEKK模型少很多,但是其估计过程仍然比较复杂。简单起见,我们事先指定估计模型的滞后阶数,使用AR(3)-GARCH(1,1)模型估计每类资产的条件方差,动态相关系数矩阵只使用DCC(1,1)模型估计。
此外,在之前的研报中我们发现压缩估计类模型中的样本单位阵线性压缩模型(LsI)和等相关系数线性压缩模型(LsCORR),在设定的实验场景下实践效果较好,因此,我们额外加入这两个模型作为条件协方差矩阵估计方法与无条件协方差矩阵估计方法的对比。
协方差估计模型的评价方法
本文分别选取国内股票、行业、大类资产和全球股、债、商品等大类资产2007年以来的真实数据来滚动构建最低波动组合或目标波动组合,考察组合样本外表现,其中:
1. 股票维度,全市场筛选满足如下条件的股票:
a) 2007年以前成立;
b) 2007年至2020年5月,股票最长停牌时间不超过10天,因为停牌会导致收益率为零,影响波动率的估计;
c) 非ST股;
筛选过后一共剩余232支股票,在实证中,从这232支股票中随机抽取50支来研究不同资产维度下各类协方差估计量的表现。
2. 行业维度,选取28个申万一级行业作为考察对象。
3. 国内大类资产维度,选取常规的股、债、商资产作为考察对象。
a)股票包括沪深300、中证500、中证1000、恒生指数、标普500;
b) 债券包括中债-新综合财富指数、中债-国债总财富指数、中债-信用债总财富指数、中债-企业债总财富指数;
c) 商品包括CRB综合现货指数、南华商品指数、伦敦金现、伦敦银现、布伦特原油。
4.全球股指维度,选取全球主要国家的七种股指类资产组合,包括沪深300、欧洲股指、日经股指、纳斯达克指数、英国富时100、MSCI新兴市场指数和澳洲股指。
5. 全球债券指数维度,选取全球主要国家的六种债券类资产组合,包括澳洲、德国、日本、美国、英国、中国十年期国债期货。
6.全球商品指数维度,选取标普高盛商品指数,包括能源、金属和农业这三种商品指数
7.全球大类资产维度,选取4、5、6的组合代表全球大类资产。
最低波动组合样本外表现
理论上,当协方差估计量越精确时,资产间的相关性刻画越贴近真实情形,构建的最低波动组合的样本外波动也应该越小。
实证过程中,我们在每月末基于历史数据估计协方差,然后基于优化模型求解最低波动组合对应的最优权重,构建下个月的持仓,最后统计整个回测区间内组合的年化波动率。需要说明的是,组合优化过程中,始终保持权重和为1的约束,对于是否加入卖空约束,我们分别作了实证。
有限制卖空约束的最低波动模型如下
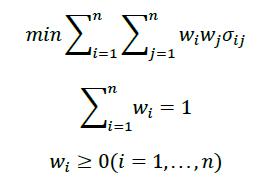
无限制卖空约束的最低波动模型如下
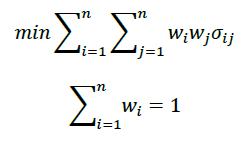
目标波动组合样本外表现
采用与最低波动组合相似的构建思路,我们同时实证了目标波动组合的样本外表现。该测试场景对结构化产品设计具有较高的实用价值,比如一个挂钩目标波动策略的期权产品,目标波动控制得是否精准直接影响到期权的定价。理论上,当协方差估计量越精确时,目标组合样本外的波动率与初始设置的目标波动越匹配。
同样地,我们在每月末基于优化模型构建最新持仓,但是目标波动组合中不能加入权重和为1的约束,否则优化问题可能无法收敛,而对于是否加入卖空约束,我们分别作了实证。
有限制卖空约束的目标波动模型如下
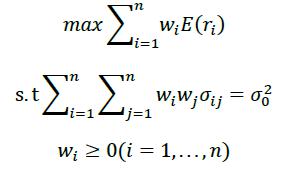
其中,E(ri)为估计窗口内收益率均值,采用估计窗口内历史数据计算;
无限制卖空约束的目标波动模型如下
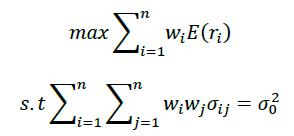
不同估计方法在多场景下的实证分析
采用2007年以来股票、行业、国内大类资产、全球股指、全球债券指数、全球商品指数和全球大类资产作为输入,每月末基于指定窗宽的历史数据计算各类协方差估计量,进而基于优化模型求解最低波动组合(或目标波动组合)对应的权重,构建投资组合,最后考察整个回测区间内组合的年化波动率来评估协方差估计量的优劣。理论上,当协方差估计量越精确时,资产间的相关性刻画越贴近真实情形,构建的最低波动组合(或目标波动组合)的全局年化波动率也应该越小(或越接近目标值)。实证过程中有如下细节需要说明:
1. 最小波动组合中,无论采用何种协方差估计量,组合优化过程中,始终保持权重和为1的约束;目标波动组合中,由于各类资产的波动水平不一,优化过程中不能设置权重和为1的约束,否则优化问题可能无法收敛;
2. 对于是否加入卖空约束,我们分别作了实证。
3. 宽下回测结果的可比性。
下图展示了各类测试场景下组合的年化波动率,如果协方差估计量相比于样本协方差有改善,则数值用红色标注。针对七种资产组合的不同场景,进行如下分析。
国内股票场景

随着观察窗口长度提升,无条件协方差的估计误差逐渐增大;但是Barra半衰期模型没有出现这种现象,USE4S模型表现更好,可能是因为其半衰期取值相对较小,使得久远的样本权重较低,这在一定程度上降低了久远数据带来的估计误差,更适用于日度数据的处理。同时,Barra模型将方差和相关系数矩阵分开估计,进而得到最终的条件协方差矩阵。考虑到股票的波动程度大,方差差异较大,易造成更大的估计误差,因此单独估计方差对结果的改善非常有效。Riskmetrics模型在股票场景下表现不佳,可能因为股票市场的波动较大,使得历史样本的无效性增强。Riskmetrics2006模型是对多个Riskmetrics1996模型的再次加权平均,本质上二者原理相同,对样本协方差虽有微弱的改善但同样不甚理想。多元GARCH 模型的表现明显依赖于估计窗宽,CCC模型与DCC模型都仅在最大的窗宽内有效。由于DCC模型考虑了相关系数的动态变化,样本外的年化波动率要低于CCC模型,但即使在最长的回测窗口里,其表现依然弱于Barra半衰期模型。
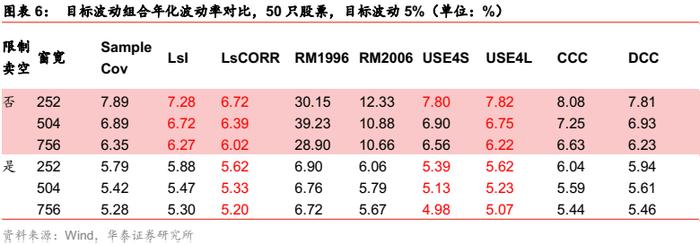
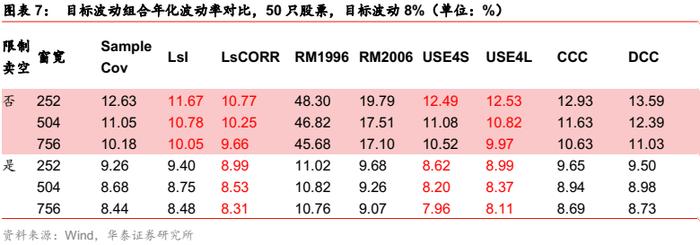
目标波动场景下,5%与8%这目标波动组合与最小波动组合结果类似,即Riskmetrics 模型和多元GARCH模型的表现明显逊于Barra半衰期模型,即使使用了最长的估计窗宽。然而,与最小波动组合不同的是,在无卖空限制的情形下,压缩估计的表现优于Barra半衰期模型。Barra半衰期模型在有卖空限制下同样有所改善,但总体而言,在国内股票场景下,条件协方差相比压缩估计并无明显优势。
国内行业场景
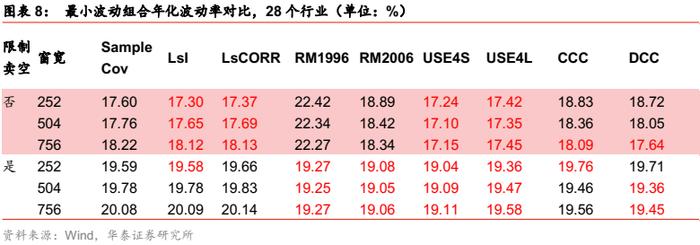
行业场景下,Barra半衰期模型相比样本协方差的提升同样明显,并且估计误差未随窗宽增长而增大,而无条件协方差估计却延续了这一劣势。
Riskmetrics模型在限制卖空条件下表现较好,上篇报告中我们已提到:在优化模型里添加卖空约束等价于对协方差矩阵进行某种特殊的压缩,因此,添加卖空约束可能无法真实地评估各类协方差估计量的精准性。且限制卖空条件下也并无明显优势。
多元GARCH模型在行业场景下依然全面弱于Barra半衰期模型,并且在不限制卖空时,对协方差估计精度的提升仅对应于最长的窗宽。尽管添加卖空约束后扩大了协方差估计误差,但无论是CCC模型还是DCC模型,相对样本协方差的改善都非常微弱。
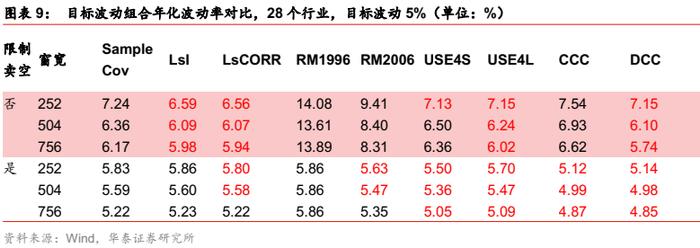
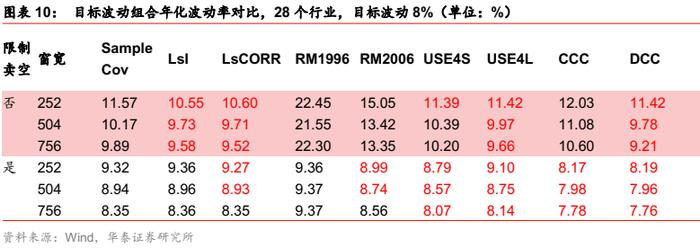
在行业场景下,移动平均模型中,Barra半衰期模型对样本协方差的改善比Riskmetrics 模型更明显;多元GARCH模型与Barra无显著差异。无条件协方差和条件协方差对比,压缩估计在无卖空限制下优于条件协方差,在限制卖空条件下逊于条件协方差。
我们认为,目标波动组合的实际应用价值更高。总体而言,针对国内行业场景,类似国内股票场景下,条件协方差相比压缩估计并无明显优势,特别是在无卖空限制下。
国内大类资产场景
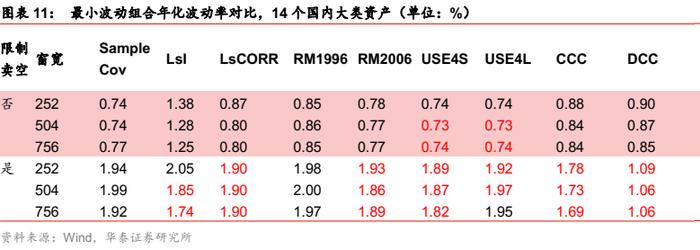
国内大类资产场景下,Barra半衰期模型表现仍然出色,优于Riskmetrics模型。多元GARCH模型中的DCC模型在限制卖空的条件下表现较好,甚至超过了Barra半衰期模型和压缩估计。非限制卖空条件下,样本协方差本身已经能达到较好的效果,其他各估计模型均无明显改善,仅Barra模型有微弱提升。
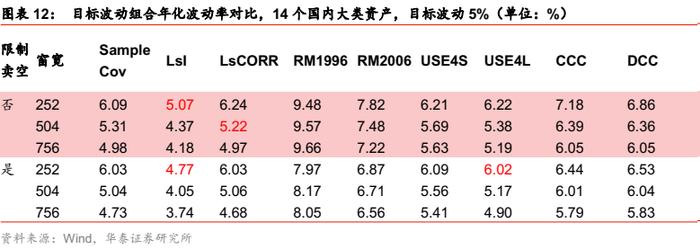
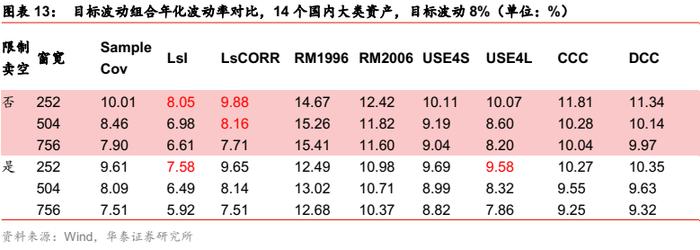
对于目标波动组合,无论是否限制卖空,样本协方差均可以在某个窗口下基本达到目标波动水平,误差小,提升空间不大。Riskmetrics模型、Barra半衰期模型以及多元GARCH模型都没有显著的改善效果。压缩估计对样本协方差在某些特定的窗口下有所改善。整体而言,该场景下提升空间不大,采用样本协方差,通过调整窗口,即可获得较好表现。
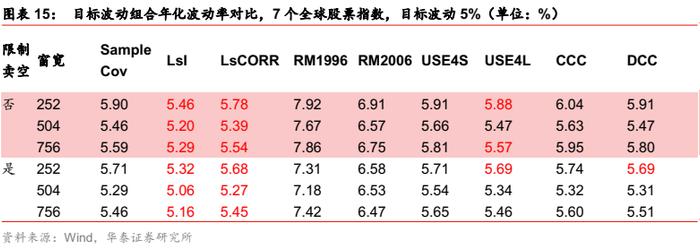
全球股指场景
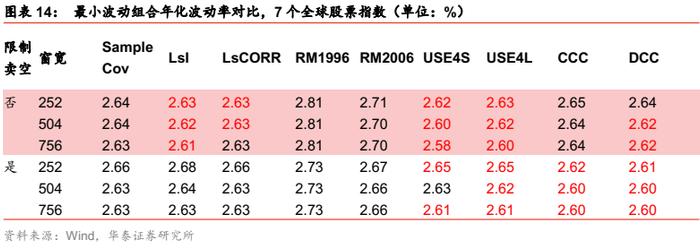
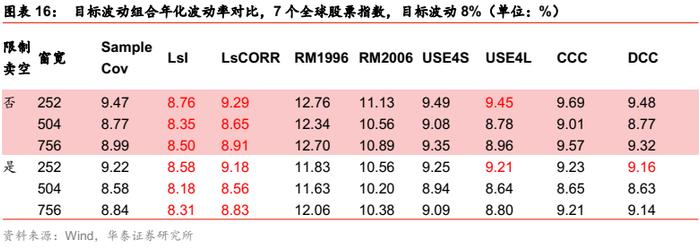
对于最小波动组合,各类估计方法都没有明显改进,与样本协方差相差无几。对于目标波动组合,压缩估计有明显改进。这一结论与国内个股、行业非限制卖空场景下基本一致。
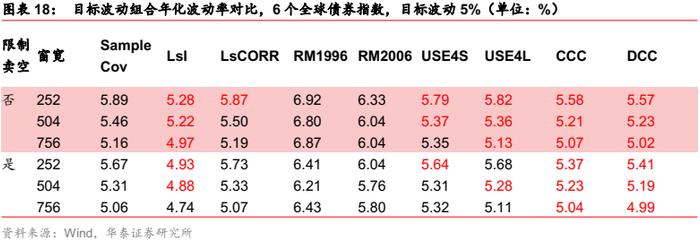
全球债券指数场景

对最小波动组合,各类协方差估计方法都没有明显提升,Barra模型和多元GARCH模型有微弱改善。
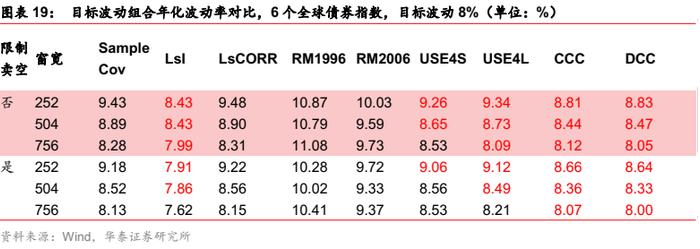
对目标波动组合,样本协方差的估计精度随窗口增长而提高。在756天的窗口下,样本外非常接近目标波动水平,消除历史信息无效性的需求不强,仅DCC模型的表现较好;而在窗口较短时,样本协方差精度较低,压缩估计、Barra、多元GARCH模型均有所改善,压缩估计模型略优。
总体而言,债券场景下消除历史信息无效性的需求不强,压缩估计或者多元GARCH模型都较为适用。
全球商品指数场景
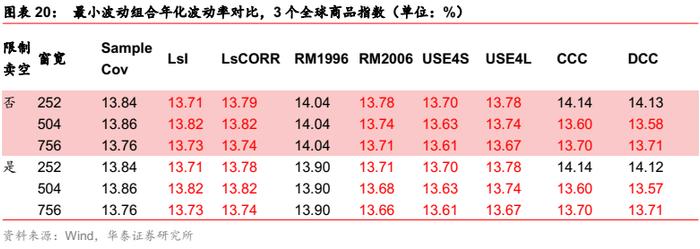
对于最小波动组合,三类条件协方差估计方法大部分有所改善,且优于压缩估计。
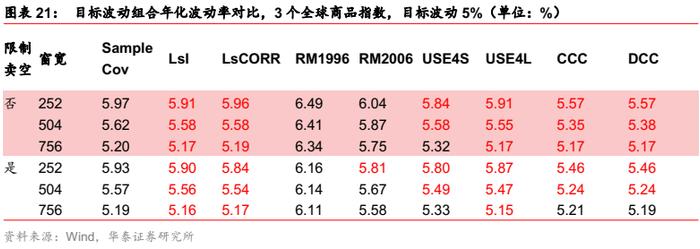
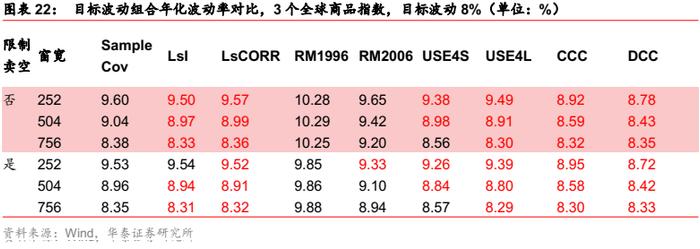
对于目标波动组合,无论是否限制卖空,多元GARCH模型的改善都较明显,两种Barra半衰期模型的表现均好于Riskmetrics模型,其中USE4S模型更胜一筹。
全球大类资产场景
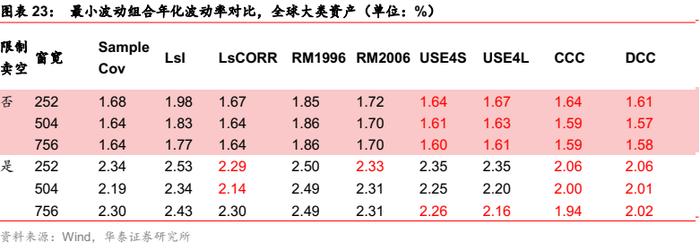
对于最小波动组合,多元GARCH模型提升最明显,Barra模型也在部分窗口下有所改进。
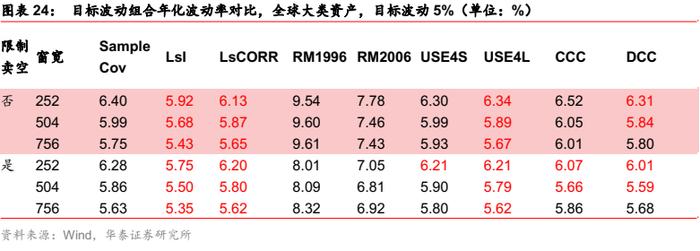
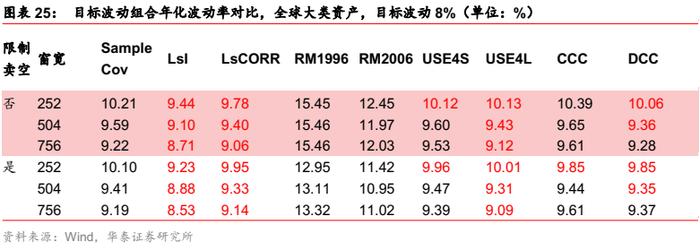
对于目标波动场组合,样本协方差有较大提升空间。但估计误差并未随窗口增长而增大,说明消除历史信息无效性的需求并不强。压缩估计的改善最明显,多元GARCH模型和Barra模型也在部分参数下有所改进,但不如压缩估计明显。
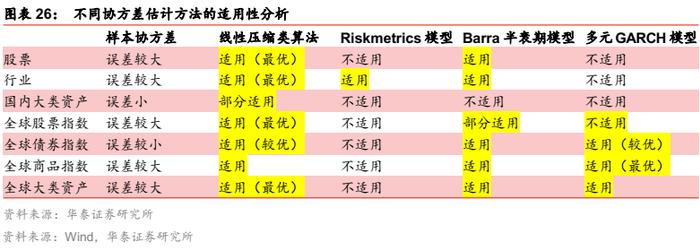
小结
以目标波动组合、无卖空限制下的结论为准,不同协方差估计方法的适用性汇总如下:
总结与展望
本文实证了样本协方差、线性压缩模型、Riskmetrics模型、Barra半衰期模型、多元GARCH模型在内的多种协方差估计方法,对投资组合的协方差估计提出了一些有实操意义的结论。
为什么需要引入条件协方差估计方法?在考虑金融市场时变性的情况下,资产的波动率和相关性往往会呈现出时变规律,与无条件协方差矩阵不随时间变化,也即每期观测变量之间是独立同分布的假设相矛盾。因此,我们需要引入条件协方差矩阵,加入过去信息作为已知条件,这更符合真实的金融建模场景。
三类条件协方差估计方法的效果如何?Barra半衰期模型能够在大部分资产组合场景下有效改善协方差矩阵参数估计的时效性和估计精度,Riskmetrics模型只在少数场景下适用,明显弱于Barra。多元GRACH模型在国内场景并不适用,在海外资产组合上有一定效果,特别在消除历史信息无效性的需求不强的场景下,比其他条件协方差估计方法表现更好。
Riskmetrics模型适用于什么场景? Riskmetrics1996模型和Riskmetrics2006模型本质上都是指数加权平均法,而Riskmetrics2006模型是对多个不同频率的Riskmetrics1996模型的再次加权平均,更加具有普适性。结果显示,两种Riskmetrics模型对估计误差的减小都不太理想。仅通过Riskmetrics模型难以对协方差估计起到显著的改善。
Barra半衰期模型适用于什么场景?Barra半衰期模型的适用性在条件协方差中最广,除了在目标波动组合的国内大类资产场景下没有提升,在剩余六种资产组合场景下均有一定改善。Barra半衰期模型的核心在于将方差和相关系数矩阵分开估计,进而得到协方差矩阵。可见,方差的单独估计对准确度的提高尤为重要。
多元GRACH模型适用于什么场景?本文实证的多元GARCH模型CCC、DCC,其分开估计的思想与Barra半衰期模型类似,但条件方差使用一元GARCH模型估计,条件相关系数有常相关与动态相关两种假设,投资者可以根据自己的主观判断合理选择。特别在消除历史信息无效性的需求不强的场景下,比其他条件协方差估计方法表现更好。
两种协方差估计的改善方向各自有什么优劣? 条件协方差估计更适合于构建最小波动组合,在本文实证的各类资产场景中,以Barra半衰期模型为代表的条件协方差估计量在降低样本外波动率方面都具有明显优势。究其原因,是条件协方差的估计误差不随窗宽的延长而增大。而在构建目标波动组合时,很多场景下,样本协方差本身的估计误差并不随窗宽的延长而线性增大,条件协方差估计量的优势反而减弱,压缩类算法对样本协方差的改善最为明显。
风险提示
本报告对历史数据进行梳理总结,不构成任何投资建议。根据历史数据的规律总结,存在失效的可能。市场发生超预期波动,导致拥挤交易。
参考文献
1. Olivier Ledoit, Michael Wolf. “A well-conditioned estimator for large-dimensional covariance matrices.” Journal of Multivariate Analysis. 2004 88(2): 365-411.
2. Olivier Ledoit, Michael Wolf. “Honey, I Shrunk the Sample Covariance Matrix.” The Journal of Portfolio Management. 2004 30(4): 110-119.
3. Robert F. Engle, Olivier Ledoit, Michael Wolf. “Large Dynamic Covariance Matrices” Journal of Business and Economic Statistics. 2017 37(2): 365-375.
4. Jagannathan R, Ma T. Risk Reductio in Large Portfolios Why Imposing the Wrong Constraints Helps[J]. the NATIONAL BUREAU of ECONOMIC RESEARCH. 2003 58(4): 1651-1684.
5. Valeriy Zakamulna. Test of Covariance-Matrix Forecasting Methods[J]. The Journal of Portfolio Management. 2015 41(3): 97-108.
6. Menchero J, D. J. Orr, and J Wang. The Barra US Equity Model(USE4). MSCI Barra Research Notes. (2011)
7. Kevin Sheppard. Financial Econometrics Notes. (2019)
8. Ruey S. Tsay. Analysis of Financial Time Series(ThirdEdition). (2012)
免责声明与评级说明
公众平台免责申明
本公众号不是华泰证券股份有限公司(以下简称“华泰证券”)研究报告的发布平台,本公众号仅供华泰证券中国内地研究咨询服务客户参考使用。其他任何读者在订阅本公众号前,请自行评估接收相关推送内容的适当性,且若使用本公众号所载内容,务必寻求专业投资顾问的指导及解读。华泰证券不因任何订阅本公众号的行为而将订阅者视为华泰证券的客户。
本公众号转发、摘编华泰证券向其客户已发布研究报告的部分内容及观点,完整的投资意见分析应以报告发布当日的完整研究报告内容为准。订阅者仅使用本公众号内容,可能会因缺乏对完整报告的了解或缺乏相关的解读而产生理解上的歧义。如需了解完整内容,请具体参见华泰证券所发布的完整报告。
本公众号内容基于华泰证券认为可靠的信息编制,但华泰证券对该等信息的准确性、完整性及时效性不作任何保证,也不对证券价格的涨跌或市场走势作确定性判断。本公众号所载的意见、评估及预测仅反映发布当日的观点和判断。在不同时期,华泰证券可能会发出与本公众号所载意见、评估及预测不一致的研究报告。
在任何情况下,本公众号中的信息或所表述的意见均不构成对任何人的投资建议。订阅者不应单独依靠本订阅号中的内容而取代自身独立的判断,应自主做出投资决策并自行承担投资风险。订阅者若使用本资料,有可能会因缺乏解读服务而对内容产生理解上的歧义,进而造成投资损失。对依据或者使用本公众号内容所造成的一切后果,华泰证券及作者均不承担任何法律责任。
本公众号版权仅为华泰证券所有,未经华泰证券书面许可,任何机构或个人不得以翻版、复制、发表、引用或再次分发他人等任何形式侵犯本公众号发布的所有内容的版权。如因侵权行为给华泰证券造成任何直接或间接的损失,华泰证券保留追究一切法律责任的权利。华泰证券具有中国证监会核准的“证券投资咨询”业务资格,经营许可证编号为:91320000704041011J。
华泰金工深度报告一览




