来源:华泰金融工程
S0570516010001SFC No. BPY421 研究员
陈 烨 S0570518080004 研究员
李子钰 S0570519110003 研究员
何 康 S0570520080004 研究员
报告发布时间:2020年8月28日
摘要
WGAN模型可应用于金融资产时间序列生成,效果优于原始GAN模型
本文探讨GAN模型的一类重要变体——WGAN,并将其运用于金融资产时间序列的生成,发现WGAN在生成数据的真实性和多样性上均优于原始GAN。原始GAN模型具有训练不同步、训练损失函数不收敛和模式崩溃的缺点。WGAN模型使用Wasserstein距离衡量真实分布与生成分布之间的距离,克服了原始GAN模型中JS距离的缺陷。使用GAN和WGAN生成上证综指日频和标普500月频收益率序列,结果表明GAN无法复现出真实序列的长时程相关等特性,WGAN则有显著改善,并且WGAN在多样性上相比于GAN也有一定提升。
W距离克服了JS散度的缺陷,在生成对抗网络中是更合适的距离指标
原始GAN模型的主要缺点是判别器D和生成器G训练不同步、训练损失函数不收敛和模式崩溃。其中训练不同步问题与JS散度的梯度消失现象有关;模式崩溃由KL散度的不对称性导致;损失函数不收敛由GAN本身D和G的博弈导致。W距离避免了JS散度带来的梯度消失现象,故而不用再小心平衡D和G的训练过程。WGAN用判别器近似估计真假分布间的W距离,随着训练的进行,W距离越来越小,即判别器的损失函数收敛,可以辅助指示训练进程。因此相比于JS散度和KL散度,W距离是应用于生成对抗网络里更合适的衡量分布间“距离”的指标。
WGAN生成序列在“真实性”上相比于GAN模型有进一步的提升
数据实证部分围绕WGAN与GAN模型的对比展开,我们选取上证综指日频和标普500月频的对数收益率序列进行生成训练并展示结果。除自相关性、厚尾分布、波动率聚集、杠杆效应、粗细波动率相关、盈亏不对称性这六项指标以外,本文还引入方差比率检验、长时程相关的Hurst指数两项指标验证生成序列的真实性。在上证综指日频序列上,GAN生成序列在Hurst指标上与真实序列仍有差距,WGAN则有显著改善;在标普500月频数据上,GAN生成序列在波动率聚集、粗细波动率相关和盈亏不对称性指标上表现不佳,WGAN也改善明显,更接近真实序列。
WGAN生成序列在不失真的基础上相比于GAN生成序列更加多样
另外我们引入衡量序列相似性的DTW指标,评价生成序列的多样性。在上证综指日频序列上,WGAN生成序列多样性相较于GAN有小幅提升;在标普500月频数据上,WGAN生成序列多样性相较于GAN有明显提升。我们看到的不再是重复的生成序列,而是观察到了更多的市场可能性。
风险提示:WGAN生成虚假序列是对市场规律的探索,不构成任何投资建议。WGAN模型存在黑箱问题,深度学习存在过拟合的可能。深度学习模型是对历史规律的总结,如果市场规律发生变化,模型存在失效的可能。
研究导读
本文是华泰金工生成对抗网络(GAN)系列的第二篇,关注GAN的重要变式——WGAN。在前序研究《人工智能31:生成对抗网络GAN初探》(20200508)中,我们指出GAN网络可以生成“以假乱真”的股指收益率时间序列,多项统计指标表明GAN生成序列的质量优于对照组模型。WGAN是GAN的经典变式之一,将GAN中的JS散度替换成Wasserstein距离(简称W距离),在图像生成等领域被证明效果优于GAN。本文将展示WGAN在生成模拟金融资产数据中的应用,并对比WGAN与GAN的生成效果。
GAN的生成样本表现已较为优秀,但是理论推导及实践结果均表明GAN存在固有缺陷。我们的目标是希望模型能简单高效地生成逼真且多样化的样本,以模拟市场的多种可能性。然而GAN模型存在的训练不收敛、判别器与生成器训练不同步、模式崩溃等问题使得目标难以完美实现。GAN模型仍具有改进空间,WGAN正是为应对GAN的缺陷而提出的变式。
相比于GAN模型使用的JS散度,WGAN使用W距离衡量目标的生成分布与真实分布之间的远近。Martin Arjovsky等学者对JS散度的研究表明,GAN的缺陷大多数与JS散度有关,JS散度可能并不适用于生成对抗网络,W距离是更合适的选择。WGAN的主要改变正是引入W距离,核心思想是用判别器估计生成分布与真实分布的W距离,用生成器拉近W距离,以达到生成样本逼近真实样本的目标。
本文分为理论与实践两部分展示WGAN。理论部分探讨GAN的缺点,并通过对比的方式介绍WGAN的原理和算法。实践部分从生成样本的“真实性”和“多样性”两个角度出发,比较WGAN和GAN的生成结果,实证结果表明WGAN的生成样本质量相较于GAN改善明显。
生成对抗网络GAN的缺点
GAN的缺点回顾
在引入WGAN之前,我们首先讨论GAN模型的缺点,主要包括以下三方面:
1. 生成器G和判别器D训练不同步问题。生成器与判别器的训练进度需要小心匹配,若匹配不当,导致判别器D训练不好,则生成器G难以提升;若判别器D训练得太好,则生成器G训练容易梯度消失,难以训练。
2. 训练不收敛问题。生成器G与判别器D相互博弈,此消彼长,训练过程中任何一方的损失函数都不会出现明显的收敛过程,我们只能通过观察生成样本的的好坏判断训练是否充分,缺少辅助指示训练进程的指标。
3. 模式崩溃(Mode Collapse)问题。GAN模型的生成样本容易过于单一,缺乏多样性。注意样本单一并不一定导致样本失真:GAN生成的收益率序列表现出的经验特征与真实序列十分接近,但并不代表生成序列包含市场可能出现的各种情况。
GAN缺点一:G和D训练不同步
一方面,由于生成器与判别器的“博弈”关系,如果判别器训练得不好,无法给真假样本作出公允评判,那么生成器将无法得到正确反馈,生成水平无法得到提升,生成数据质量大概率较低。
另一方面,判别器训练得太好也会阻碍生成器的训练,原因分以下两步骤讨论:
1. JS散度的进一步探讨;
2. 训练生成器梯度消失。
JS散度的进一步探讨
首先我们对JS散度进行简要回顾。JS散度和KL散度均可衡量两个分布p和q之间的距离,其中JS散度定义在KL散度的基础上,解决了KL散度不对称的问题。二者定义为:
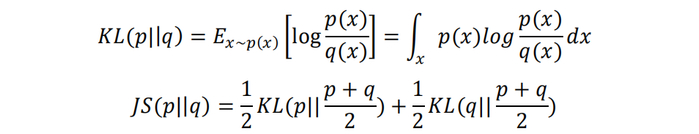
GAN使用JS散度衡量真实分布pr与生成分布pg间的距离,模型的训练过程近似等价于最小化JS(pr||pg),随着JS散度越来越小,生成分布逼近真实分布,生成样本则越来越拟真,最终达到“以假乱真”的效果。
当两个分布有重合部分时,分布离得越近,JS散度越小;当两个分布完全重合时,JS散度取值为零。JS散度的特殊性质体现在,当两个分布无重合部分时,分布离得越远,并不意味着JS散度一定越大。严谨的表述为:如果pr和pg的支撑集相交部分测度为零,则它们之间的JS散度恒为常数log2:
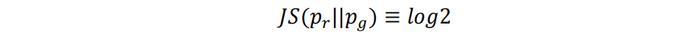
上述命题的精确解释及证明过程请参考附录部分。该命题的通俗解释是,如果pr和pg不相交或者近似不相交(即支撑集相交部分测度为零),那么JS散度恒为常数log2。这个结论意味着只要pr和pg不重合,那么无论二者距离多远,JS散度都为常数,如下图的State1和State2所示。换言之,此时JS散度失去了判别距离远近的能力。GAN训练时如果判别器训练太好,往往就会出现这种情况,阻碍生成器的训练,我们在下一小节详细展开。
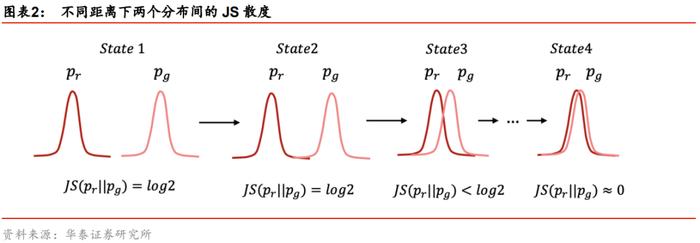
训练生成器梯度消失
为叙述清晰,我们再次展示原始GAN模型的目标函数:
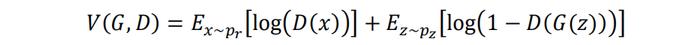
或者可以直接写成下述目标函数形式,其中pr表示真实分布,pg表示生成分布:
在《人工智能31:生成对抗网络GAN初探》(20200508)中我们证明对于给定的生成器G,如果判别器D训练到最优,则训练生成器的损失函数将变成:
上式中的JS散度导致生成器难以训练。事实上,拓扑学理论可以证明,大部分情况下生成分布与真实分布二者的支撑集相交部分的测度是零,即绝大部分情况下两个分布不相交或者近似不相交。那么根据JS散度的性质可以推出,在判别器达到最优的情况下,优化生成器的损失函数会变成常数,而常数的梯度恒为零。换言之,此时训练生成器会出现严重的梯度消失问题。
从更直观的角度而言,判别器最优时,JS散度只能告诉生成器当前的生成分布与真实分布距离远,但是到底距离多远?JS散度无法告诉生成器答案,因此只要生成分布与真实分布近似不重合,那么二者差很远或较接近对生成器没有任何区别,损失函数梯度都是零,生成器自然难以训练。
在实际训练过程中,我们毕竟难以达到理论上的“最优判别器”,但是Arjovsky等(2017)指出,随着判别器接近最优,生成器损失函数的梯度仍会接近于零,出现梯度消失现象:
我们对GAN的缺点一进行总结:GAN在训练过程中如果判别器训练得不好,则生成器难以提升;如果判别器训练得太好,再去训练生成器容易产生梯度消失的问题,导致生成器难以训练。
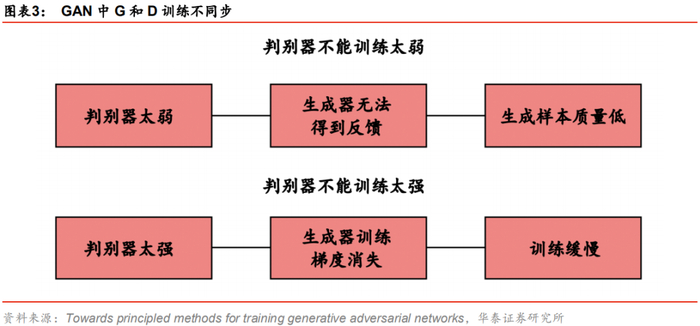
GAN缺点二:训练不收敛
从逻辑上说,生成器G和判别器D始终处于相互博弈、相互提升的过程中,因此无法看到任何一方的损失函数收敛,损失函数无法提供有意义的指导价值。从损失函数表达式出发,可以更清晰地观察不收敛的过程。
在原始的GAN中,我们实际训练判别器和生成器使用的损失函数分别为下面两式。判别器的损失函数J(D)在GAN原始目标函数前加负号,是因为训练中默认使用梯度下降法最小化损失函数。生成器损失函数J(G)只有J(D)的第二项,是因为在训练生成器时,log(D(x))不包含G且D固定,相当于常数,故略去。
在训练时每轮迭代优化判别器,使得J(D)减小,即要求Ez~pz[log(1-D(G(z)))]增大;优化生成器,使得J(G)减小,即要求Ez~pz[log(1-D(G(z)))]减小。一方增大而一方减小,即判别器与生成器的损失函数优化过程相背离,无法看到任何一方收敛。
GAN缺点三:模式崩溃
GAN在生成时容易出现生成样本过于单一,缺乏多样性的现象,这种现象称为模式崩溃。例如在生成手写数据集样本时,某种结构的GAN生成结果如下图所示。模型最终只生成手写数字“6”,虽然形态十分逼真,但显然不是我们想要的生成模型。
在论证模式崩溃的问题之前,我们首先引入Non-saturating GAN的概念。在原始的GAN目标函数中包含Ez~pz[log(1-D(G(z)))],由于log(1-D(G(z)))在训练初期梯度太小,因此在实践中我们更常使用−Ez~pz[log(D(G(z)))]代替上面这项,此时判别器与生成器的损失函数分别为:
这种形式的GAN称为Non-saturating GAN,原始的GAN称为Minimax GAN,二者在网络对抗的思想上一致,但Non-saturating GAN更便于解释模式崩溃的问题。以下我们分两步论述模式崩溃:
1. Non-saturating GAN生成器损失函数的等价表达;
2. 模式崩溃的原因。

Non-saturating GAN中J(G)的等价表达
前文我们已经提到,在Minimax GAN模型中,如果判别器达到最优(不妨假设为D*(x)),那么训练生成器的目标函数将变为:
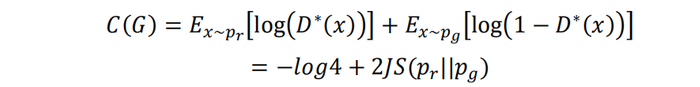
对应的最优判别器表达式为:
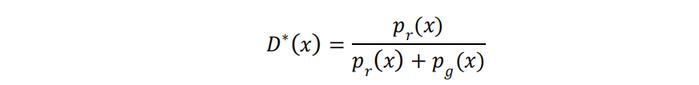
下面我们考虑生成分布与真实分布的KL散度:
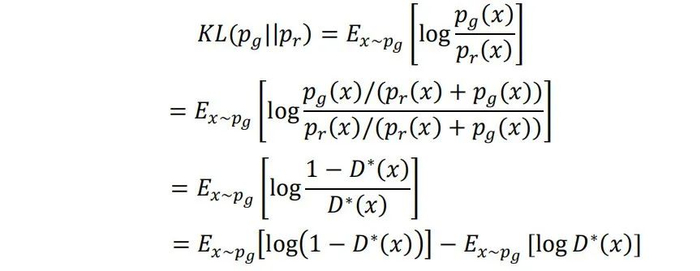
联立C(G)的表达式,我们可以得到Non-saturating GAN中生成器损失函数的等价表达为:
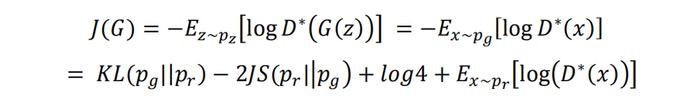
由于在训练生成器时完全依赖于判别器的损失函数项为常数可以忽略,因此简化的等价表达为:
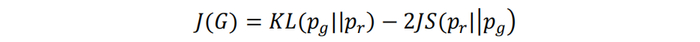
注意,上述表达式的前提是判别器达到最优。实际上,当GAN训练到后期,判别器的能力已经很强,可近似认为判别器接近最优。因此,训练生成器近似于最小化上述J(G)的表达式。生成器的模式崩溃正是由J(G)的第一项KL散度的不对称性导致。
模式崩溃的原因
基于上文J(G)的等价表达式可以进一步推导出模式崩溃的原因。首先将KL散度写成积分的形式:
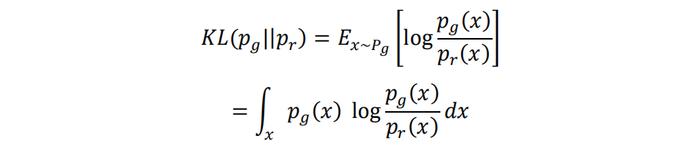
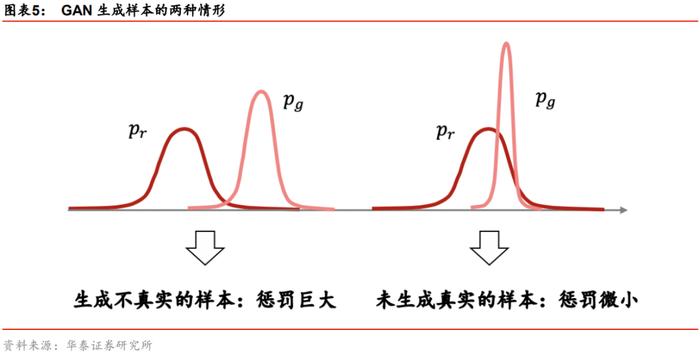
我们考虑生成样本的两种情形:
1. 生成器生成了不真实的样本。对应于那些不真实的样本,pg(x)>0但pr(x)≈0,此时KL散度中间的被积项将会趋于∞;
2. 生成器没能生成真实的样本。对应于没能生成的那些真实样本,pr(x)>0但pg(x)≈0,此时KL散度中间的被积项将会趋于0。
Non-saturating GAN中优化生成器的损失函数要求KL散度尽量小。由于第一种情形损失接近无穷,惩罚巨大,生成器就会避免生成不真实的样本;由于第二种情形损失接近零,惩罚微小,因此生成器完全有可能只生成单一的真实样本,而不生成更多不同的真实样本。生成单一的真实样本已经足够“安全”,生成器没有必要冒着失真的风险生成多样化的样本,模式崩溃问题由此产生。
Wasserstein GAN介绍
Wasserstein距离
从上一章可知,GAN的大部分缺陷与JS散度有关,因此JS散度可能不适用于GAN。Arjovsky等(2017)提出使用Wasserstein距离(简称W距离)替代JS散度,这样构建的生成对抗网络称为Wasserstein GAN(简称WGAN)。
W距离的通俗解释
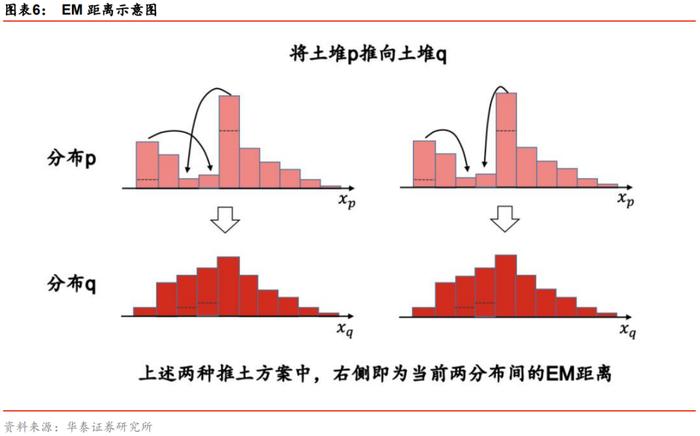
W距离用来衡量两个分布之间的远近,也称为“推土机距离”(Earth Mover Distance,后文简称EM距离),这个名称十分形象。如果将两个分布p和q分别比作两堆土,那么我们可以有不同的方式将土堆p推到和土堆q相同的位置和形状。如下图所示,我们展示两种将土堆p推成土堆q的方案,很显然这两种方式的平均推土距离(以推土量为权重,推土距离的加权和)不相等。EM距离表示在所有推土方案中,平均推土距离最小的方案对应的推土距离。
从“推土”的角度出发,EM距离的表达式如下所示:
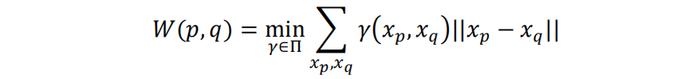
其中𝛾(xp, xq)表示某种推土方案下对应的xp到xq的推土量,||xp-xq||则表示二者之间的某种距离(如欧式距离),Π表示所有可能的推土方案。根据EM距离的直观定义可知,EM距离没有上界,随着两个分布之间越来越远,EM距离会趋于无穷。换言之,EM距离和JS散度不同,不会出现梯度为零的情况。
W距离的数学定义及性质
上一小节我们从“推土”的角度定义了EM距离也即W距离,这里我们从概率分布的角度定义W距离。根据Arjovsky等(2017),衡量真实分布与生成分布的W距离数学定义如下:
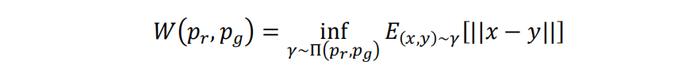
其中x~pr,y~pg,𝛾表示(x,y)的联合分布,Π(pr,pg)表示所有可能的𝛾取值空间。上式的本质是将分布pr推向分布pg所要经过的最小距离。
在论证原始的GAN模型G与D训练不同步的问题时,我们提到若真实分布与生成分布的支撑集相交部分测度为零,JS散度恒为常数。真实分布与生成分布近似不相交或者完全不相交时,那么无论真实分布与生成分布是距离一步之遥,还是距离海角天涯,JS散度都是常数。换言之,JS散度无法指示不重合的两个分布到底距离多远。
W距离的优越性正体现于此。W距离随分布间“距离”的变化是连续的,即使两个分布完全不相交,W距离也不会收敛到常数,而是随分布间“距离”的增加而不断增大,直至无穷。因此,W距离没有梯度消失的问题,可以用W距离替代GAN中的JS散度。
Wasserstein GAN的原理
WGAN的原理
W距离的原始数学定义过于理论,且在实际中无法直接计算。为便于使用,可以通过Kantorovich-Rubinstein Duality公式(Arjovsky, 2017)将其等价变换为下式:
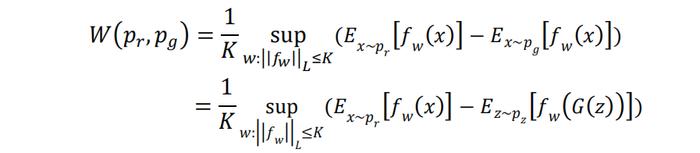
关于这个等价定义,我们进行如下三点解释:
1. {𝑓𝒘(x), 𝒘∈W}表示一族依赖于参数𝒘的函数𝑓,参数𝒘的取值空间为W。函数𝑓可以是能写出表达式的简单初等函数,也可以是一个复杂的深度学习网络。如果𝑓是一个深度学习网络,则参数w就是网络中的一系列权重。
2. 𝒘:||𝑓𝒘||≤𝐾表示函数𝑓𝒘满足Lipschitz条件:即对于𝑓𝒘定义域内的任何取值𝑎和𝑏,满足,|𝑓𝒘(a)-𝑓𝒘(b)| ≤𝐾|a-b|,𝐾称为Lipschitz常数。在W距离的等价定义式中,𝐾可以是任意正实数。
3. sup表示对所有满足条件的函数𝑓𝒘求括号中表达式的上确界,在实际应用中近似等价于求括号中表达式的最大值。
W距离的等价定义式实际上就是WGAN的目标函数。在给定生成器G时,上述定义式中的函数𝑓𝒘可以用一个深度学习网络来代替,这个深度学习网络的目标就是要最大化Ex~pr[𝑓𝒘(x)]−Ez~pz[𝑓𝒘(G(z))],在训练时𝐾是一个常数,因此系数项可以忽略。为保持与GAN统一,这里我们仍称这个深度学习网络为“判别器”(原文称为critic),当然此时“判别器”已不再执行判别真假的功能,而是估计真假样本分布的W距离。类似于GAN,WGAN在实践中判别器与生成器也是交替训练的,这里我们列出二者的损失函数:
在原始的GAN模型里,判别器的作用本质上也是在估计生成分布与真实分布之间的距离(用JS散度衡量),然后用生成器去拉近JS散度。在WGAN中这种思想则更为直接:用判别器去拟合两个分布之间的W距离,用生成器去拉近W距离。
WGAN-GP的原理
WGAN的原理逻辑较清晰,但是在等价定义式中对判别器有一个重要限制——判别器需满足Lipschitz条件。通常来说有两种处理办法,一种是权重剪裁(Weight Clipping),一种是梯度惩罚(Gradient Penalty),这里分别介绍。
权重剪裁的思想是对判别器网络的权重进行限制,因为神经网络仅仅是有限个权值与神经元相乘的结果,所以如果权重在某个有限范围内变化,那么判别器的输出值𝑓𝒘(x)也不会变得太大,近似可以满足𝐾-Lipschitz条件。实际操作中,会在训练判别器的每一步反向传播更新权值之后对权重进行剪裁,例如可以将更新后的权值限制到[-0.01, 0.01]中:
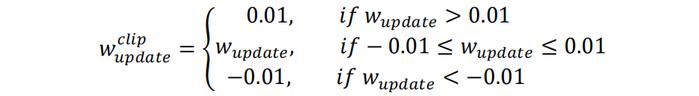
权重剪裁实际上并没有真正让判别器满足𝐾-Lipschitz条件,且实证表明权重剪裁会让大部分网络权重落在限制边界上,使得生成样本的质量不佳。
更常用的方法是梯度惩罚。如果能将判别器𝑓𝒘相对于输入x的梯度限制在一定范围内,那么自然𝑓𝒘就能满足𝐾-Lipschitz条件。根据这个思想,可以在判别器损失函数中增加惩罚项,将判别器损失函数写成:
这个损失函数对判别器𝑓w相对于输入的梯度进行惩罚,将梯度的L2-范数约束在1附近,从而保证Lipschitz条件的成立。通过这种改进的WGAN模型就称为WGAN-GP模型(Gulrajani,2017)。这里我们进行额外几点说明:

WGAN-GP的训练算法
在WGAN-GP的实际训练过程中,判别器D与生成器G交替进行训练,一般判别器D训练K次,生成器G训练1次。基于前文的分析, WGAN-GP训练算法的伪代码如下所示。

GAN与WGAN的比较
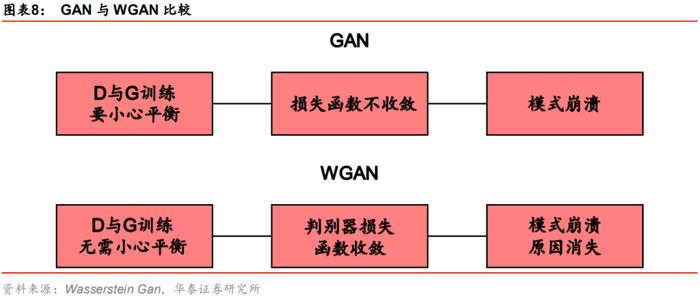
本小节我们分析WGAN是否针对GAN的三项缺点有所改进。
1. GAN的判别器D与生成器G训练进程必须小心平衡,否则会出现训练不同步的问题。一般每轮迭代D训练K次,G训练1次,对于GAN我们要重点调整K的值,避免判别器太好或太差;对于WGAN则无需小心调整K,可以让判别器的训练进度适当快于生成器。即使判别器D训练得很好,再去训练生成器也不会出现梯度消失的问题。例如,在实践中每轮迭代可以令D训练5次,再令G训练1次。
2. GAN模型D和G的损失函数都不收敛,无法指示训练进程。在WGAN中,因为判别器的损失函数是在近似估计真假样本分布之间的W距离,随着训练的推进,这个W距离会存在收敛的过程,可以辅助指示训练的进程。
3. GAN模型容易产生模式崩溃的问题。前文我们提到,模式崩溃主要和KL散度以及JS散度有关,在WGAN中JS散度被替换成W距离,因此导致GAN发生模式崩溃的原因在WGAN中也就消失了。但值得注意的是,这并不意味着WGAN生成的样本完全没有模式崩溃的可能性。
方法
在实证部分,我们围绕GAN与WGAN的对比展开实验,展示在生成金融时间序列上WGAN相对于GAN的改进。在展示结果之前,我们同样对训练数据、网络构建和评价指标进行说明。此外我们还引入衡量序列相似性的指标,用来判别样本的多样性。这里特别说明,由于WGAN-GP的梯度惩罚方法在实际应用中生成效果更好,因此本文数据测试均基于WGAN-GP模型,后文提到WGAN也均指代WGAN-GP,不作严格区别。
训练数据
为方便后续对比,本文选取《人工智能31:生成对抗网络GAN初探》(20200508)中具有代表性的指数日频及月频对数收益率进行训练建模,标的和数据起止日期如下。

与GAN建模时相同,在处理真实样本时,采用滚动的方式对原始的对数收益率数据进行采样。例如对于上证综指原始近16年的时序数据,滚动生成长度为2520个交易日(约为10年)的样本,那么真实样本约有1500条。
网络构建
相比于GAN模型,WGAN在网络结构上的主要改动在于判别器最后的输出层没有进行sigmoid激活。这是因为GAN模型中的判别器需要对真假样本进行判别,最后的输出必须是0~1之间的值,表示输入样本是真实样本的概率。而WGAN中的判别器作用是拟合生成分布与真实分布间的W距离,所以网络不应对输出值进行0~1的限制。
此外在构建判别器网络时,由于判别器的损失函数加入了梯度惩罚项,且梯度惩罚项对每一个输入样本的梯度进行限制,因此在判别器的网络结构中不应该加入Batch-Normalization(批归一化,简称BN)层,BN会将同一批其他样本的信息融入到对单个样本的梯度计算中,破坏样本间的独立性,此时算出来的梯度并不是真实的判别器对单个样本的梯度。一般可以使用Layer-Normalization层或者不使用任何归一化层。
参考Pardo等(2019)文献,我们构建如下生成器G与判别器D。生成器G含有四个卷积层及一个输出层,每两个卷积层之间含一个上采样层;判别器D含有三个卷积层、两个全连接网络层及一个输出层,每两个卷积层之间含一个最大值池化层。


结合WGAN判别器的收敛情况及生成数据的质量,本文选择的上证综指日频数据训练迭代次数为1500次,标普500月频的训练迭代次数为1000次,相比于GAN模型的2000次,训练时间开销显著降低。在WGAN中我们不再需要小心平衡判别器与生成器的训练次数,每轮迭代可以令判别器多训练几次,本文设定每轮迭代中判别器D训练5次,生成器G训练1次。

序列真实性指标
在评估GAN生成序列的质量时我们介绍了6项指标:自相关性、厚尾分布、波动率聚集、杠杆效应、粗细波动相关和盈亏不对称性,具体定义可以参考《人工智能31:生成对抗网络GAN初探》(20200508)报告,这里不再展开。
为更好地评估生成序列的真实程度,除上述6项指标外,我们额外引入2类衡量真实序列特征的指标,最后将WGAN与GAN各自生成的虚假序列在这8项指标上与真实序列进行对比,观察WGAN的生成序列相对于GAN模型是否有所改进。
方差比率检验
方差比率检验(Variance Ratio Test)最早提出是为了检验金融资产的价格序列是否为随机游走,从而验证市场的有效性。检验的核心思想在于,如果市场是有效的,那么资产价格服从随机游走,则收益率的方差是时间的线性函数,下面我们展开说明。
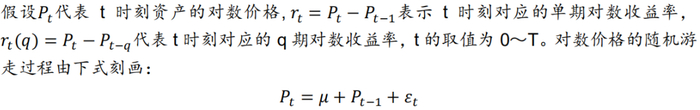
其中𝜇表示漂移项,𝜀t表示随机增量。关于𝜀t的不同假设可以得到不同强度的随机游走,例如我们可以假设𝜀t非自相关,且同方差。此时:
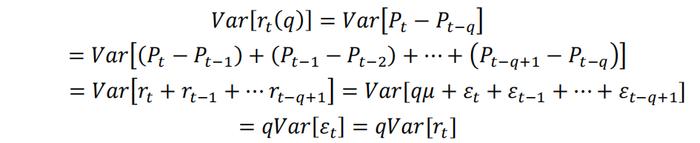
即在随机游走假设下,Var[rt(q)]= qVar[rt]成立,q期的对数收益率方差等于单期对数收益率方差的q倍,因此可以用如下方差比率检验来判断市场的随机游走假设是否成立。
Lo和Mackinlay等(1988)提出统计量Z(q)对此进行检验,Z(q)的具体计算公式请参考附录。如果H0假设成立,即q期的对数收益率方差等于单期对数收益率方差的q倍,那么在大样本条件下Z(q)服从N(0,1)标准正态分布,95%置信水平下的拒绝域为(-∞, 1.96]∪[1.96, +∞)。因此,对于真实序列和生成的每条样本序列,我们可以遵循如下步骤进行方差比率检验:
1. 选定需要检验的滞后阶数q,计算样本的单期对数收益率序列;
2. 计算检验统计量Z(q);
3. 将Z(q)与拒绝域临界值进行比较,例如在95%的置信水平下,如果-1.96≤Z(q) ≤1.96,则接受原假设,认为当前序列在q期的时间跨度内为随机游走,否则为非随机游走。
一般来说,A股市场在短期内不能拒绝原假设,会表现出随机游走的特征,在中长期则拒绝原假设,表现出非随机游走的特征。
长时程相关
时间序列的长时程相关(Long-Range Dependence)指的是时间序列过去的状态可能对现在或未来产生影响。对于金融时间序列,长时程相关则意味着间隔较久的证券价格之间也存在相关性,在这种假设下,市场可能会产生“历史重演”的现象,因此长时程相关也称为长记忆性。Hurst指数可以刻画这种长时程相关,其定义如下:
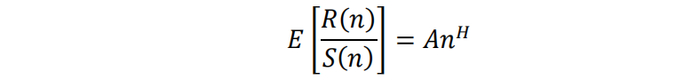
其中n表示某一段序列的区间长度,R(n)表示这一段序列在区间上的变化范围,S(n)表示这一段序列在区间上的波动,A表示某一个常数,H表示Hurst指数。在实际计算过程中我们正是按照Hurst指数的定义来计算的,这种计算方法也叫做R/S分析法(Rescaled Range Analysis),计算步骤如下图所示。

如果Hurst > 0.5,则表示时间序列具有长记忆性;如果Hurst < 0.5,则表示时间序列具有反持续性,表现出均值回复的特征,波动较强;如果Hurst = 0.5,则表示时间序列随机游走。A股及美股市场指数对数收益率序列的Hurst值在0.5~0.6之间,表现出较弱的长记忆性。
评价指标小结
这里我们对总计8项评价生成序列质量的指标进行总结,如下表所示。

序列相似性指标
从理论上来说,WGAN消除了GAN模式崩溃的原因,那么WGAN生成样本的多样性是否有所提升?要回答这个问题,我们首先需要找到合适的衡量序列多样性的指标。
本文采用动态时间规整指标(Dynamic Time Warping,简称DTW)进行衡量,这一指标源于语音识别和匹配领域,可用于匹配两段内容相似但是语速不同的语音片段。由于语速不同,相同时刻的内容差别可能比较大,用传统的欧式距离去衡量相同时刻的距离很可能得出两条片段不相似的结论。
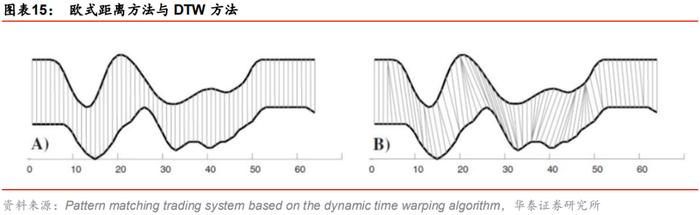
如果两段金融时间序列整体趋势相同,但是在时间轴上存在伸缩或变形,如左下图所示,粗线代表两条序列,细线代表对应时点求欧式距离,那么此时计算对应时刻的欧式距离再求和就不是合适的距离度量指标。
DTW算法是对欧式距离的改良,它并不直接计算序列在相同时刻的欧式距离之和,而是找到趋势最为匹配的时间点然后计算彼此间的距离,一条时间序列上的某个点可能对应另一条时间序列上的多个点,如右下图所示。即使时间序列在时间尺度上有拉长或压缩,DTW也能把握序列整体的趋势,从而判定两条序列总体相似或者不相似,这样的方法也称为时间序列的形态匹配。
DTW基于动态规划算法寻找每一步最匹配的两个点,规划的递推公式如下:
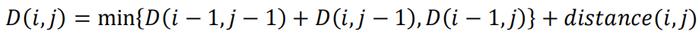
我们称两条序列分别为A和B。上式中等式左侧的D(i,j)表示直到序列A的第i个时刻和序列B的第j个时刻两条序列的累积DTW距离;等式右侧的distance(i,j)则表示序列A的第i个点和序列B的第j个点之间的欧式距离。如果两条序列长度均为N,则最终D(N,N)就表示两条序列的累积DTW距离。
两条序列之间的DTW指标越小,表示两条序列越相似,反之则表示两条序列越不相似。我们希望WGAN的生成序列具备多样性,序列间的DTW值越大越好。
WGAN与GAN结果对比
本章对比WGAN和GAN的生成效果。实验表明,WGAN的生成效果优于GAN,体现在两方面:1. WGAN生成数据质量更好,在长时程相关等统计指标上相较于GAN更接近真实序列;2. WGAN在生成样本多样性上相较于GAN有提升。WGAN的优势在标普500月频序列生成上体现更为明显。
上证综指日频序列
损失函数及真假序列展示
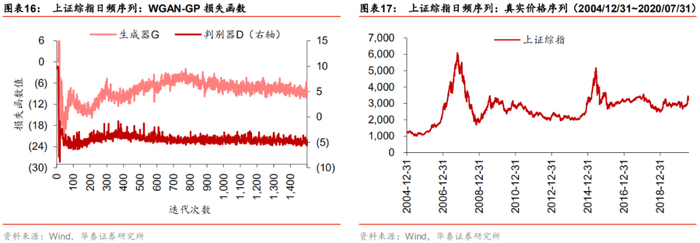
左下图展示WGAN模型在训练过程中生成器G与判别器D的损失函数。可以看到判别器的损失函数在100轮迭代次数以内从一个较大的值迅速减小,在200~700轮迭代之间上下波动,700轮后收敛,在较窄范围内波动。生成器的损失函数没有明显的收敛过程。根据判别器损失函数的指示及生成序列的质量,最终我们选择1500轮迭代次数进行训练。
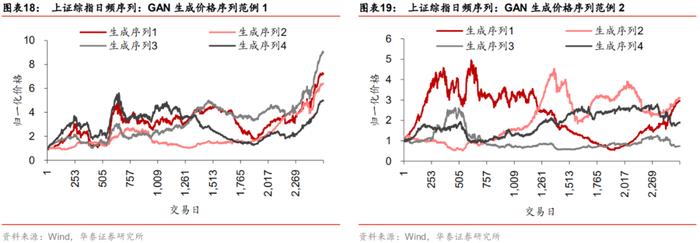
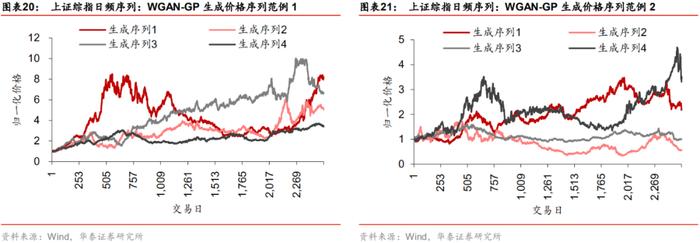
评价指标对比
这里我们将上证综指日频真实序列、WGAN和GAN生成序列的8项指标进行对比。首先考察前6项指标,GAN与WGAN各自分别生成1000条虚假序列计算评价指标并求其均值,结果如下所示。WGAN和GAN的生成序列都较完美地复现出上证综指日频序列在自相关性、厚尾分布、波动率聚集、杠杆效应、粗细波动率相关及盈亏不对称性上的特征。
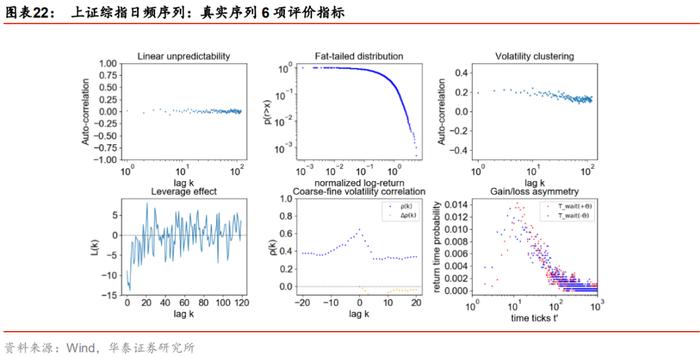
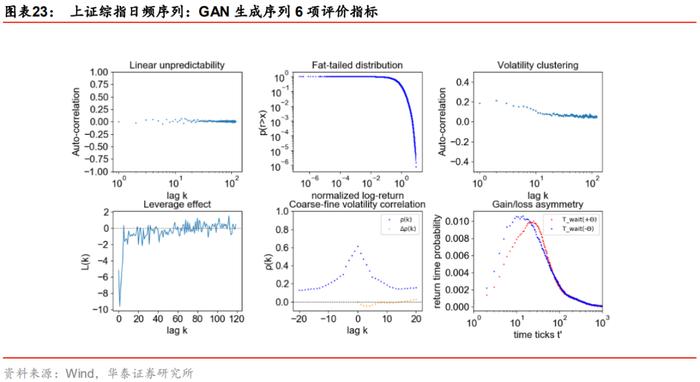
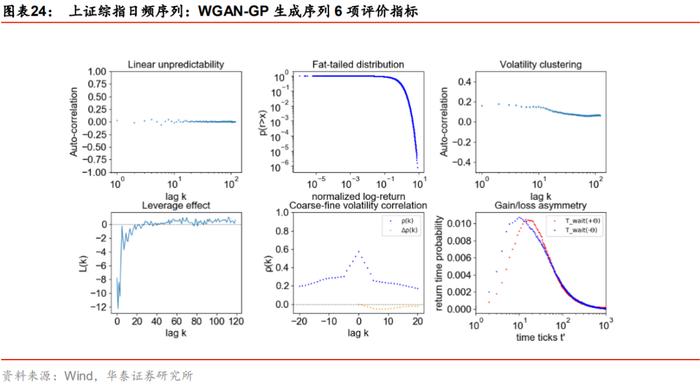
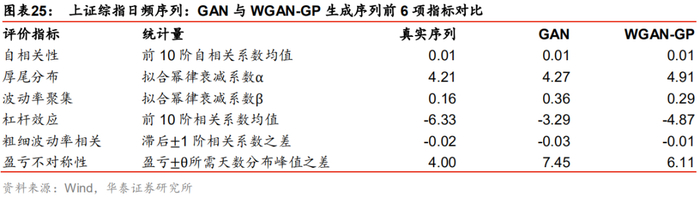
在前6项评价指标上WGAN与GAN模型旗鼓相当,下面我们继续展示在补充的2项指标上二者的表现。下图是两模型在方差比率检验上的结果,其中蓝色虚线表示真实序列各阶的方差比率检验统计值,箱线图表示1000条生成序列在各阶的方差比率检验统计值的分布;表格为两个模型各自1000条生成序列在各阶方差比率检验统计量的均值。
真实序列表现出的特征是短期(对应阶数2~10)随机游走,即低阶方差比率检验统计量落在[-1.96,1.96]的范围内;高阶(对应阶数50~100)非随机游走,即高阶方差比率检验统计量落在[-1.96,1.96]的范围外。总体来说,GAN与WGAN的生成序列都复现出了这一特征,但左图蓝线在箱形外沿,右图蓝线贴近箱形均值,说明WGAN生成序列的方差比检验统计量与真实序列更为接近。
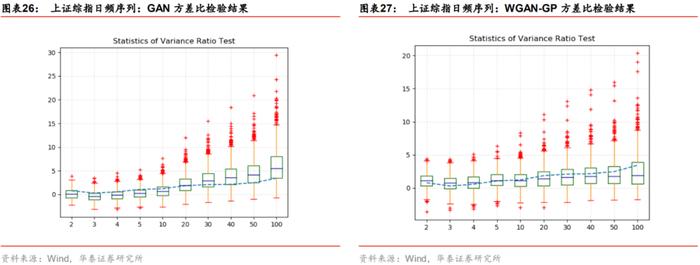

GAN与WGAN生成序列的Hurst指数值如下图所示。上证综指日频序列的真实Hurst值为0.52,表现出弱长时程相关的特征。GAN模型生成序列中大部分的Hurst指数都小于0.5,仅有约20% Hurst值大于0.5。WGAN模型生成序列则有显著改善,约有60%的Hurst值大于0.5,可以看到WGAN生成序列的Hurst值整体分布位于GAN的右侧。
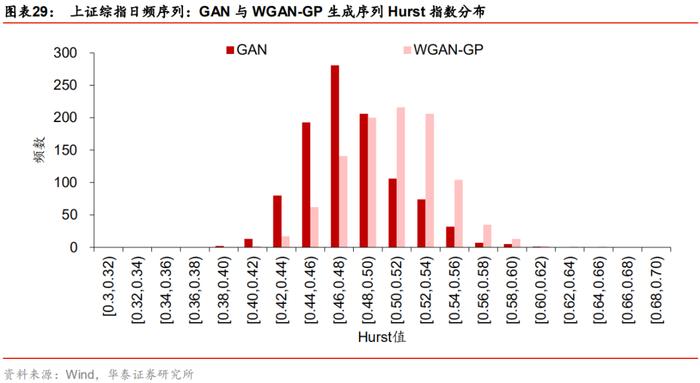
然而仅根据表现出长时程相关的序列比例判定生成序列是否失真是不够的,这里对生成序列的Hurst值进行假设检验。我们想要验证生成分布在Hurst指标上的总体均值是否显著大于0.5,假设𝜇H表示生成分布在Hurst指标上的总体均值,则原假设和备择假设为:
生成的1000条虚假序列相当于从生成分布总体中的采样,对于这样的大样本检验,我们可以直接使用单样本正态总体均值的单边显著性检验统计量,如下所示:

在大样本(一般来说样本数大于30)条件下,原假设H0成立时U服从N(0,1)标准正态分布,因此在95%置信水平下,U如果落入(-∞, -1.64]的拒绝域,则拒绝原假设,认为生成样本的Hurst指数总体均值小于0.5。
在上述假设检验下,GAN与WGAN生成的1000条序列检验结果如下表所示。GAN模型1000条生成序列的Hurst均值假设检验统计量为-657.02,远小于-1.64,因此有理由相信GAN模型生成序列在长时程相关上是失真的。WGAN模型检验统计量为192.27,充分远离拒绝域,因此可以合理认为WGAN生成序列复现了真实序列的长时程相关特征。

样本多样性
我们从GAN模型生成的1000条上证综指日频假序列中随机抽取1000组配对序列,计算这1000组配对序列之间的DTW指标,对WGAN生成序列也进行同样的操作。两个模型的DTW分布如下图所示。整体上看来,WGAN生成样本序列之间的DTW值分布位于GAN右侧,DTW值更大,即意味着序列之间的相似性更低,多样性略有提升。
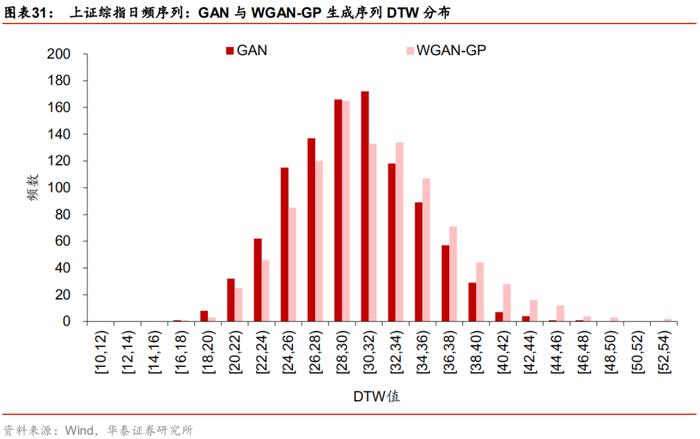
标普500月频序列
损失函数及真假样本展示
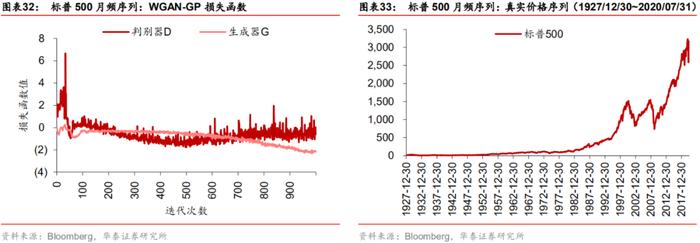
WGAN模型的训练损失函数如左下图所示。判别器损失函数在前100次迭代时迅速降低,在100~700次迭代期间先减后增,700次迭代以后收敛到一个较小的范围内。结合损失函数的形态及生成数据的质量,我们最后选取1000轮迭代次数进行训练。生成器的损失函数同样没有明显的收敛过程。
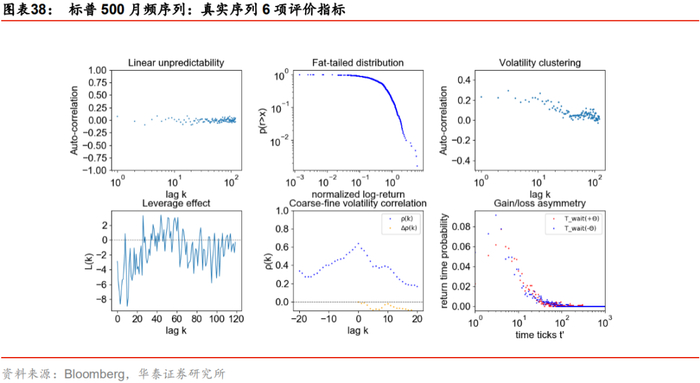
图表34~37展示两类模型生成的标普500月频部分数据,左侧序列与右侧序列分别是不同尺度上随机抽取的4组虚假序列。从净值图可知,WGAN生成样本相对于GAN生成样本更为丰富,内部差异更大,而不是完全“复制”真实序列的单调上升趋势。
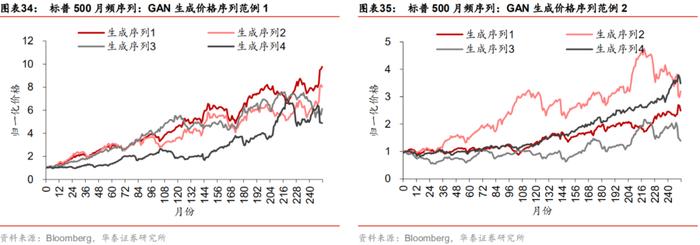
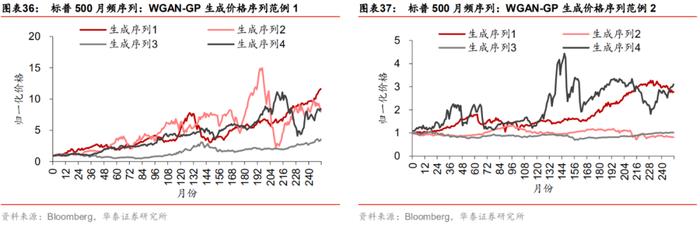
评价指标对比
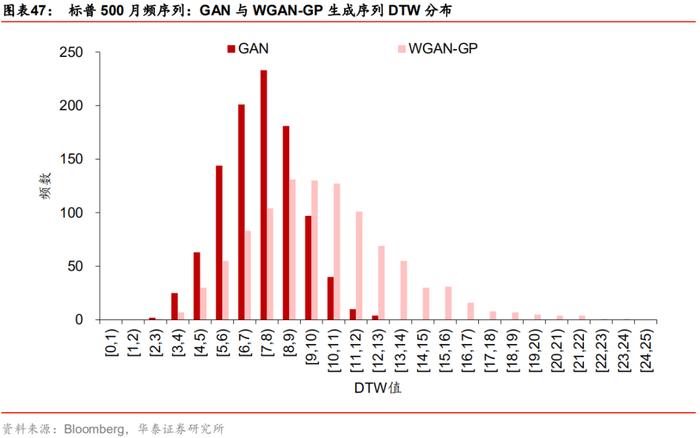
真实序列、WGAN与GAN生成序列的前6项评价指标如下图所示。GAN生成序列在波动率聚集指标上没有表现出明显的衰减过程;在粗细波动率相关指标上虽然表现出预测能力的不对称性,但是不对称性与真实序列正好相反;在盈亏不对称性指标上没能表现出涨得慢、跌得快的特征,即红色分布未明显分布在蓝色分布右侧。
相比之下,WGAN生成序列有明显改善。WGAN生成序列的波动率聚集指标表现出一定的衰减特征;粗细波动率相关指标橙色点在低阶为负,与真实序列的不对称性一致;在盈亏不对称性指标上红色分布峰值位于蓝色分布峰值右侧,表现出涨得慢、跌得快的特征。
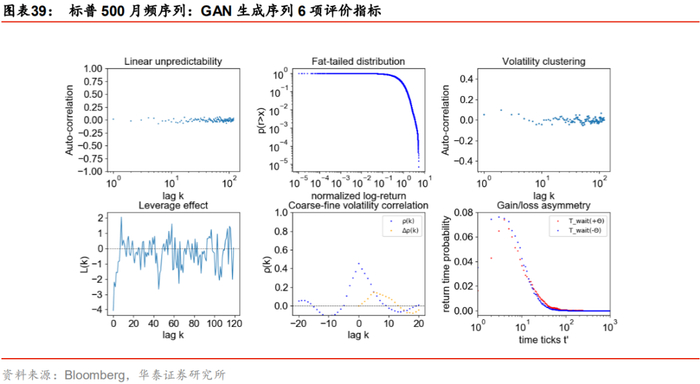
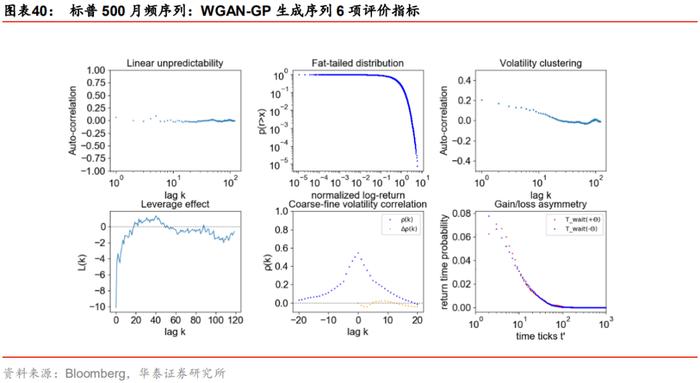
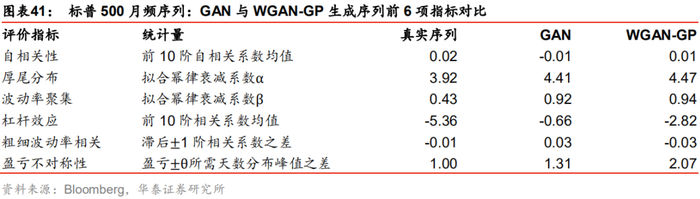
两组模型生成序列在方差比率检验上的结果如下所示。标普500月频真实序列在全阶数上均表现出随机游走的特征,整体上来说GAN模型与WGAN模型的生成序列也都复现出了随机游走的性质,即方差比率检验统计量均落入[-1.96,1.96]范围内。但是GAN生成序列的方差比率检验结果与真实序列仍有偏差,在20~50阶左右表现尤为明显,此时代表真实序列的蓝色虚线完全偏离在箱形图之外。相比之下,WGAN的方差比率检验结果则与真实序列更为接近。
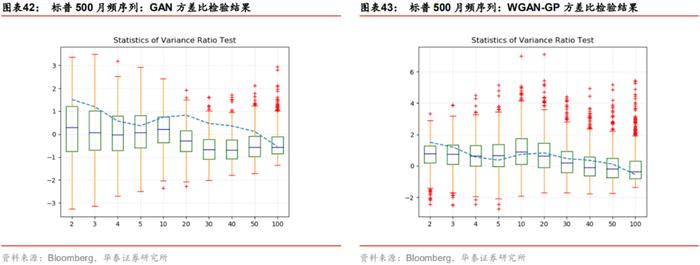

两组模型生成序列在Hurst指数上的分布如下所示。标普500月频对数收益率序列的Hurst指数为0.60,表现出长记忆性。WGAN序列和GAN生成序列的Hurst指数均有超过70%大于0.5。对两组生成序列Hurst值的假设检验结果表明,两组生成序列Hurst指数总体均值显著大于0.5,WGAN与GAN生成的标普500月频序列均复现出真实序列的长时程相关性。
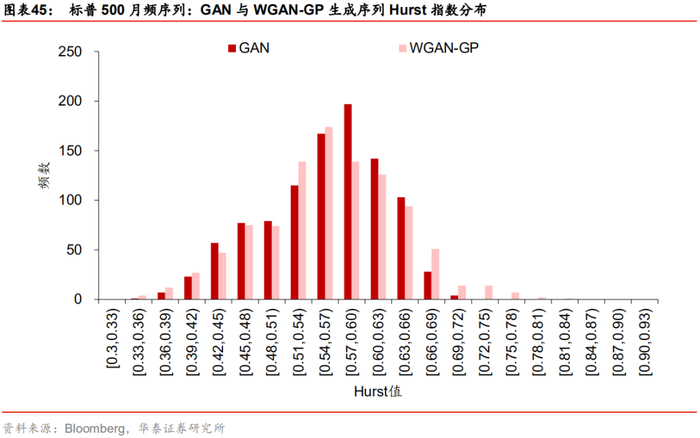

样本多样性
相比于GAN生成序列,WGAN生成序列肉眼看起来多样性有明显提升,并且多样性的提升建立在生成序列特征更接近于真实序列的基础上。为量化多样性,我们仍然在两组生成样本内各随机抽取1000组配对序列并计算DTW指标,结果如下图所示。WGAN生成序列之间的DTW值分布明显位于GAN模型生成序列的右侧,说明WGAN生成序列的多样性相比于GAN模型有显著提升。
评价指标汇总
我们对两种模型在上证综指日频和标普500月频上的生成序列评价指标进行总结,如下图所示。其中前1~7项指标均表示真实序列表现出了对应特征,第8项方差比率检验指标含义如下:上证综指日频真实序列低阶随机游走,高阶非随机游走;标普500月频真实序列全阶数随机游走。


总结与讨论
本文探讨GAN模型的一类重要变体——WGAN在生成金融时间序列中的应用并与GAN进行比较。不同于GAN模型中的JS散度,WGAN模型使用Wasserstein距离衡量训练过程中真实分布与生成分布之间的“距离”。每一步训练迭代中用判别器D估计两个分布之间的W距离,用生成器G拉近W距离,目标是使得真实分布与生成分布越来越接近,以此达到生成“以假乱真”样本的目的。WGAN的训练过程比GAN更加方便快捷,且生成序列在真实性和多样性上相比GAN有显著提升。
原始GAN模型的主要缺点是判别器D和生成器G训练不同步、训练损失函数不收敛和模式崩溃。其中训练不同步问题与JS散度的梯度消失现象有关;模式崩溃由KL散度的不对称性导致;损失函数不收敛由GAN本身D和G的博弈导致。W距离避免了JS散度带来的梯度消失现象,故而不用再小心平衡D和G的训练过程。WGAN用判别器近似估计真假分布间的W距离,随着训练的进行,W距离越来越小,即判别器的损失函数收敛,可以辅助指示训练进程。因此相比于JS散度和KL散度,W距离是应用于生成对抗网络里更合适的衡量分布间“距离”的指标。
数据实证部分围绕WGAN与GAN模型的对比展开,我们选取上证综指日频和标普500月频的对数收益率序列进行生成训练并展示结果。除自相关性、厚尾分布、波动率聚集、杠杆效应、粗细波动率相关、盈亏不对称性这六项指标以外,本文还引入方差比率检验、长时程相关的Hurst指数两项指标验证生成序列的真实性。在上证综指日频序列上,GAN生成序列在Hurst指标上与真实序列仍有差距,WGAN则有显著改善;在标普500月频数据上,GAN生成序列在波动率聚集、粗细波动率相关和盈亏不对称性指标上表现不佳,WGAN改善明显,更接近真实序列。
另外我们引入衡量序列相似性的DTW指标,评价生成序列的多样性。在上证综指日频序列上,WGAN生成序列多样性相较于GAN有小幅的提升;在标普500月频数据上,WGAN生成序列多样性相较于GAN有明显提升。我们看到的不再是重复的美股“慢牛”序列,而是观察到了更多的市场可能性。
总的来看,WGAN模型是针对距离度量指标的改良提出的一类GAN的变体,理论及实证表明,WGAN在生成金融时序数据上相比于GAN有明显改善。在GAN的相关变式中,还有其它方向上的改良,例如针对GAN损失函数的改良(RGAN)、针对GAN原始输入数据的改良(CGAN)等,这些都是值得深入挖掘与探究的方向。
参考文献
Arjovsky, M., & Bottou, L. (2017). Towards principled methods for training generative adversarial networks. arXiv preprint arXiv:1701.04862.
Arjovsky, M., Chintala, S., & Bottou, L. (2017). Wasserstein gan. arXiv preprint arXiv:1701.07875.
Gulrajani, I., Ahmed, F., Arjovsky, M., Dumoulin, V., & Courville, A. C. (2017). Improved training of wasserstein gans. In Advances in neural information processing systems (pp. 5767-5777).
De Meer Pardo, F. (2019). Enriching Financial Datasets with Generative Adversarial Networks (Doctoral dissertation, Master’s thesis, Delft University of Technology, the Netherlands).
Campbell, J. Y., Lo, A. W., & MacKinlay, A. C. (1997). The econometrics of financial markets. Princeton University Press.
Takahashi, S., Chen, Y., & Tanaka-Ishii, K. (2019). Modeling financial time-series with generative adversarial networks. Physica A: Statistical Mechanics and its Applications, 527, 121261.
Kim, S. H., Lee, H. S., Ko, H. J., Jeong, S. H., Byun, H. W., & Oh, K. J. (2018). Pattern matching trading system based on the dynamic time warping algorithm. Sustainability, 10(12), 4641.
Lo, A. W., & MacKinlay, A. C. (1988). Stock market prices do not follow random walks: Evidence from a simple specification test. The review of financial studies, 1(1), 41-66.
Metz, L., Poole, B., Pfau, D., & Sohl-Dickstein, J. (2016). Unrolled generative adversarial networks. arXiv preprint arXiv:1611.02163.
Hurst, H. E. (1951). Long-term storage capacity of reservoirs. Trans. Amer. Soc. Civil Eng., 116, 770-799.
风险提示
WGAN生成虚假序列是对市场规律的探索,不构成任何投资建议。WGAN模型存在黑箱问题,深度学习存在过拟合的可能。深度学习模型是对历史规律的总结,如果市场规律发生变化,模型存在失效的可能。
附录
JS散度性质的证明
JS散度的性质:如果两个分布pr和pg的支撑集相交部分测度为零,则JS散度恒为常数log2,即:
我们对上述性质进行证明,首先介绍两个概念:测度和支撑集。
集合的测度:测度用来衡量Rn中子集的“大小”。以一维实数空间R中的子集为例,测度相当于是对“长度”这一概念的延伸,不仅可以描述某段连续区域的大小,即通常意义的长度概念,还可以衡量其它任意子集的“大小”。例如区间[0,1]的“大小”即为长度1,全体整数构成的集合Z的“大小”为0(虽然Z不是空集,但测度仍然为零)。
本节推导将用到测度的一个重要性质:如果函数f(x)定义域内某个子集E的测度为零,那么f(x)在E上的积分值也为零,公式表述如下所示:
随机变量的支撑集:假设随机变量ξ的概率密度函数为f(x),则ξ的支撑集(或称f(x)的支撑集)指的是ξ的所有可能取值组成的集合,即满足f(x)不为0的那些点组成的集合。例如定义在[0,1]区间上的均匀分布支撑集为[0,1],标准正态分布的支撑集为R。
下面进行证明。对于真实分布与生成分布的所有可能的取值(二者均不可能的取值对JS散度无贡献,无需考虑),我们可以划分为3部分互不相交的集合A、B、C,其中:
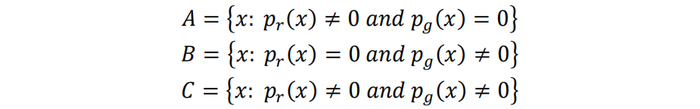
因为pr和pg的支撑集相交部分测度为零,所以集合C的测度为零。JS散度的计算等价于在上面3块集合上进行积分:
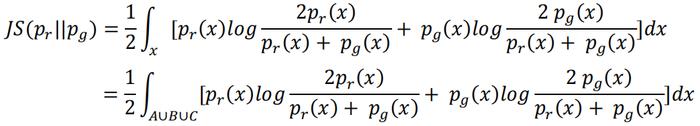
上面的式子可进一步拆分为分别在A、B、C三个集合上对中间求和项表达式进行积分,在集合A上即为:
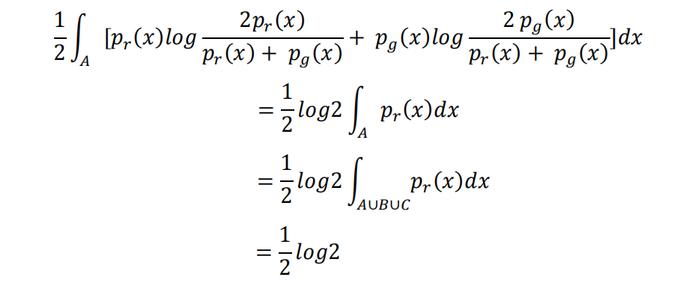
注意到在集合B上pr(x)=0,且集合C的测度为零,所以在集合B与C上对pr(x)进行积分均为零,因此上述推导中的第三行才能直接成立。类似地,在集合B上对中间求和项进行积分的结果也为1/2log2。同样由于集合C的测度为零,在集合C上对中间求和项进行积分的结果为零。因此
方差比率检验统计量计算公式
方差比率检验的原假设为:
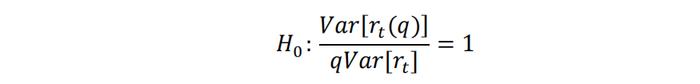
用于检验上述原假设的统计量为Z(q),q表示待检验的阶数。Z(q)的表达式如下所示:
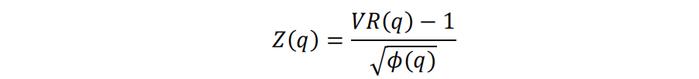
其中,分子的VR(q)是对方差比率的估计统计量,即:

免责声明与评级说明


公众平台免责申明
本公众平台不是华泰证券研究所官方订阅平台。相关观点或信息请以华泰证券官方公众平台为准。根据《证券期货投资者适当性管理办法》的相关要求,本公众号内容仅面向华泰证券客户中的专业投资者,请勿对本公众号内容进行任何形式的转发。若您并非华泰证券客户中的专业投资者,请取消关注本公众号,不再订阅、接收或使用本公众号中的内容。因本公众号难以设置访问权限,若给您造成不便,烦请谅解!本公众号旨在沟通研究信息,交流研究经验,华泰证券不因任何订阅本公众号的行为而将订阅者视为华泰证券的客户。
本公众号研究报告有关内容摘编自已经发布的研究报告的,若因对报告的摘编而产生歧义,应以报告发布当日的完整内容为准。如需了解详细内容,请具体参见华泰证券所发布的完整版报告。
本公众号内容基于作者认为可靠的、已公开的信息编制,但作者对该等信息的准确性及完整性不作任何保证,也不对证券价格的涨跌或市场走势作确定性判断。本公众号所载的意见、评估及预测仅反映发布当日的观点和判断。在不同时期,华泰证券可能会发出与本公众号所载意见、评估及预测不一致的研究报告。
在任何情况下,本公众号中的信息或所表述的意见均不构成对客户私人投资建议。订阅人不应单独依靠本订阅号中的信息而取代自身独立的判断,应自主做出投资决策并自行承担投资风险。普通投资者若使用本资料,有可能会因缺乏解读服务而对内容产生理解上的歧义,进而造成投资损失。对依据或者使用本公众号内容所造成的一切后果,华泰证券及作者均不承担任何法律责任。
本公众号版权仅为华泰证券股份有限公司所有,未经公司书面许可,任何机构或个人不得以翻版、复制、发表、引用或再次分发他人等任何形式侵犯本公众号发布的所有内容的版权。如因侵权行为给华泰证券造成任何直接或间接的损失,华泰证券保留追究一切法律责任的权利。本公司具有中国证监会核准的“证券投资咨询”业务资格,经营许可证编号为:91320000704041011J。
华泰金工深度报告一览
金融周期系列研究(资产配置)
【华泰金工林晓明团队】2020年中国市场量化资产配置年度观点——周期归来、机会重生,顾短也兼长20200121
【华泰金工林晓明团队】量化资产配置2020年度观点——小周期争明日,大周期赢未来20200116
【华泰金工林晓明团队】风险预算模型如何度量风险更有效-改进风险度量方式稳定提升风险模型表现的方法
【华泰金工林晓明团队】周期双底存不确定性宜防守待趋势——短周期底部拐头机会渐增,待趋势明朗把握或更大20191022
【华泰金工林晓明团队】二十年一轮回的黄金投资大周期——黄金的三周期定价逻辑与组合配置、投资机会分析20190826
【华泰金工林晓明团队】如何有效判断真正的周期拐点?——定量测度实际周期长度提升市场拐点判准概率
【华泰金工林晓明团队】基钦周期的长度会缩短吗?——20190506
【华泰金工林晓明团队】二十载昔日重现,三四年周期轮回——2019年中国与全球市场量化资产配置年度观点(下)
【华泰金工林晓明团队】二十载昔日重现,三四年周期轮回——2019年中国与全球市场量化资产配置年度观点(上)
【华泰金工林晓明团队】周期轮动下的BL资产配置策略
【华泰金工林晓明团队】周期理论与机器学习资产收益预测——华泰金工市场周期与资产配置研究
【华泰金工林晓明团队】市场拐点的判断方法
【华泰金工林晓明团队】2018中国与全球市场的机会、风险 · 年度策略报告(上)
【华泰金工林晓明团队】基钦周期的量化测度与历史规律 · 华泰金工周期系列研究
【华泰金工林晓明团队】周期三因子定价与资产配置模型(四)——华泰金工周期系列研究
【华泰金工林晓明团队】周期三因子定价与资产配置模型(三)——华泰金工周期系列研究
【华泰金工林晓明团队】周期三因子定价与资产配置模型(二)——华泰金工周期系列研究
【华泰金工林晓明团队】周期三因子定价与资产配置模型(一)——华泰金工周期系列研究
【华泰金工林晓明团队】华泰金工周期研究系列 · 基于DDM模型的板块轮动探索
【华泰金工林晓明团队】市场周期的量化分解
【华泰金工林晓明团队】周期研究对大类资产的预测观点
【华泰金工林晓明团队】金融经济系统周期的确定(下)——华泰金工周期系列研究
【华泰金工林晓明团队】金融经济系统周期的确定(上)——华泰金工周期系列研究
【华泰金工林晓明团队】全球多市场择时配置初探——华泰周期择时研究系列
行业指数频谱分析及配置模型:市场的周期分析系列之三
【华泰金工林晓明团队】市场的频率——市场轮回,周期重生
【华泰金工林晓明团队】市场的轮回——金融市场周期与经济周期关系初探
周期起源
【华泰金工林晓明团队】企业间力的产生、传播和作用效果——华泰周期起源系列研究之八
【华泰金工林晓明团队】耦合振子同步的藏本模型——华泰周期起源系列研究之七
【华泰金工林晓明团队】周期在供应链管理模型的实证——华泰周期起源系列研究之六
【华泰金工林晓明团队】不确定性与缓冲机制——华泰周期起源系列研究报告之五
【华泰金工林晓明团队】周期是矛盾双方稳定共存的结果——华泰周期起源系列研究之四
【华泰金工林晓明团队】周期是不确定性条件下的稳态——华泰周期起源系列研究之三
【华泰金工林晓明团队】周期趋同现象的动力学系统模型——华泰周期起源系列研究之二
【华泰金工林晓明团队】从微观同步到宏观周期——华泰周期起源系列研究报告之一
FOF与金融创新产品
【华泰金工林晓明团队】养老目标基金的中国市场开发流程--目标日期基金与目标风险基金产品设计研究
【华泰金工】生命周期基金Glide Path开发实例——华泰FOF与金融创新产品系列研究报告之一
因子周期(因子择时)
【华泰金工林晓明团队】市值因子收益与经济结构的关系——华泰因子周期研究系列之三
【华泰金工林晓明团队】周期视角下的因子投资时钟--华泰因子周期研究系列之二
【华泰金工林晓明团队】因子收益率的周期性研究初探
择时
【华泰金工林晓明团队】波动率与换手率构造牛熊指标——华泰金工量化择时系列
【华泰金工林晓明团队】A股市场低开现象研究
【华泰金工林晓明团队】华泰风险收益一致性择时模型
【华泰金工林晓明团队】技术指标与周期量价择时模型的结合
【华泰金工林晓明团队】华泰价量择时模型——市场周期在择时领域的应用
中观基本面轮动
【华泰金工林晓明团队】行业全景画像:投入产出表视角——华泰中观基本面轮动系列之五
【华泰金工林晓明团队】行业全景画像:改进杜邦拆解视角——华泰中观基本面轮动系列之四
【华泰金工林晓明团队】行业全景画像:风格因子视角 ——华泰中观基本面轮动系列之三
【华泰金工林晓明团队】行业全景画像:宏观因子视角 ——华泰中观基本面轮动系列之二
【华泰金工林晓明团队】确立研究对象:行业拆分与聚类——华泰中观基本面轮动系列之一
行业轮动
【华泰金工林晓明团队】拥挤度指标在行业配置中的应用——华泰行业轮动系列报告之十二
【华泰金工林晓明团队】基于投入产出表的产业链分析 ——华泰行业轮动系列报告之十一
【华泰金工林晓明团队】不同协方差估计方法对比分析——华泰行业轮动系列报告之十
【华泰金工林晓明团队】景气度指标在行业配置中的应用——华泰行业轮动系列报告之九
【华泰金工林晓明团队】再探周期视角下的资产轮动——华泰行业轮动系列报告之八
【华泰金工林晓明团队】“华泰周期轮动”基金组合改进版——华泰行业轮动系列报告之七
【华泰金工林晓明团队】“华泰周期轮动”基金组合构建——华泰行业轮动系列之六
【华泰金工林晓明团队】估值因子在行业配置中的应用——华泰行业轮动系列报告之五
【华泰金工林晓明团队】动量增强因子在行业配置中的应用——华泰行业轮动系列报告之四
【华泰金工林晓明团队】财务质量因子在行业配置中的应用——华泰行业轮动系列报告之三
【华泰金工林晓明团队】周期视角下的行业轮动实证分析——华泰行业轮动系列之二
【华泰金工林晓明团队】基于通用回归模型的行业轮动策略——华泰行业轮动系列之一
Smartbeta
【华泰金工林晓明团队】重剑无锋:低波动 Smart Beta——华泰 Smart Beta 系列之四
【华泰金工林晓明团队】投资优质股票:红利类Smart Beta——华泰Smart Beta系列之三
【华泰金工林晓明团队】博观约取:价值和成长Smart Beta——华泰Smart Beta系列之二
【华泰金工林晓明团队】Smart Beta:乘风破浪趁此时——华泰Smart Beta系列之一
【华泰金工林晓明团队】Smartbeta在资产配置中的优势——华泰金工Smartbeta专题研究之一
多因子选股
【华泰金工林晓明团队】华泰单因子测试之历史分位数因子——华泰多因子系列之十三
【华泰金工林晓明团队】桑土之防:结构化多因子风险模型——华泰多因子系列之十二
【华泰金工林晓明团队】华泰单因子测试之海量技术因子——华泰多因子系列之十一
【华泰金工林晓明团队】因子合成方法实证分析 ——华泰多因子系列之十
【华泰金工林晓明团队】华泰单因子测试之一致预期因子 ——华泰多因子系列之九
【华泰金工林晓明团队】华泰单因子测试之财务质量因子——华泰多因子系列之八
【华泰金工林晓明团队】华泰单因子测试之资金流向因子——华泰多因子系列之七
【华泰金工林晓明团队】华泰单因子测试之波动率类因子——华泰多因子系列之六
【华泰金工林晓明团队】华泰单因子测试之换手率类因子——华泰多因子系列之五
【华泰金工林晓明团队】华泰单因子测试之动量类因子——华泰多因子系列之四
【华泰金工林晓明团队】华泰单因子测试之成长类因子——华泰多因子系列之三
【华泰金工林晓明团队】华泰单因子测试之估值类因子——华泰多因子系列之二
【华泰金工林晓明团队】华泰多因子模型体系初探——华泰多因子系列之一
【华泰金工林晓明团队】五因子模型A股实证研究
【华泰金工林晓明团队】红利因子的有效性研究——华泰红利指数与红利因子系列研究报告之二
人工智能
【华泰金工林晓明团队】再探AlphaNet:结构和特征优化——华泰人工智能系列之三十四
【华泰金工林晓明团队】数据模式探索:无监督学习案例——华泰人工智能系列之三十三
【华泰金工林晓明团队】AlphaNet:因子挖掘神经网络——华泰人工智能系列之三十二
【华泰金工林晓明团队】生成对抗网络GAN初探——华泰人工智能系列之三十一
【华泰金工林晓明团队】从关联到逻辑:因果推断初探——华泰人工智能系列之三十
【华泰金工林晓明团队】另类标签和集成学习——华泰人工智能系列之二十九
【华泰金工林晓明团队】基于量价的人工智能选股体系概览——华泰人工智能系列之二十八
【华泰金工林晓明团队】揭开机器学习模型的“黑箱” ——华泰人工智能系列之二十七
【华泰金工林晓明团队】遗传规划在CTA信号挖掘中的应用——华泰人工智能系列之二十六
【华泰金工林晓明团队】市场弱有效性检验与择时战场选择——华泰人工智能系列之二十五
【华泰金工林晓明团队】投石问路:技术分析可靠否?——华泰人工智能系列之二十四
【华泰金工林晓明团队】再探基于遗传规划的选股因子挖掘——华泰人工智能系列之二十三
【华泰金工林晓明团队】基于CSCV框架的回测过拟合概率——华泰人工智能系列之二十二
【华泰金工林晓明团队】基于遗传规划的选股因子挖掘——华泰人工智能系列之二十一
【华泰金工林晓明团队】必然中的偶然:机器学习中的随机数——华泰人工智能系列之二十
【华泰金工林晓明团队】偶然中的必然:重采样技术检验过拟合——华泰人工智能系列之十九
【华泰金工林晓明团队】机器学习选股模型的调仓频率实证——华泰人工智能系列之十八
【华泰金工林晓明团队】人工智能选股之数据标注方法实证——华泰人工智能系列之十七
【华泰金工林晓明团队】再论时序交叉验证对抗过拟合——华泰人工智能系列之十六
【华泰金工林晓明团队】人工智能选股之卷积神经网络——华泰人工智能系列之十五
【华泰金工林晓明团队】对抗过拟合:从时序交叉验证谈起
【华泰金工林晓明团队】人工智能选股之损失函数的改进——华泰人工智能系列之十三
【华泰金工林晓明团队】人工智能选股之特征选择——华泰人工智能系列之十二
【华泰金工林晓明团队】人工智能选股之Stacking集成学习——华泰人工智能系列之十一
【华泰金工林晓明团队】宏观周期指标应用于随机森林选股——华泰人工智能系列之十
【华泰金工林晓明团队】人工智能选股之循环神经网络——华泰人工智能系列之九
【华泰金工林晓明团队】人工智能选股之全连接神经网络——华泰人工智能系列之八
【华泰金工林晓明团队】人工智能选股之Python实战——华泰人工智能系列之七
【华泰金工林晓明团队】人工智能选股之Boosting模型——华泰人工智能系列之六
【华泰金工林晓明团队】人工智能选股之随机森林模型——华泰人工智能系列之五
【华泰金工林晓明团队】人工智能选股之朴素贝叶斯模型——华泰人工智能系列之四
【华泰金工林晓明团队】人工智能选股之支持向量机模型— —华泰人工智能系列之三
【华泰金工林晓明团队】人工智能选股之广义线性模型——华泰人工智能系列之二
指数增强基金分析
【华泰金工林晓明团队】再探回归法测算基金持股仓位——华泰基金仓位分析专题报告
【华泰金工林晓明团队】酌古御今:指数增强基金收益分析
【华泰金工林晓明团队】基于回归法的基金持股仓位测算
【华泰金工林晓明团队】指数增强方法汇总及实例——量化多因子指数增强策略实证
基本面选股
【华泰金工林晓明团队】华泰价值选股之相对市盈率港股模型——相对市盈率港股通模型实证研究
【华泰金工林晓明团队】华泰价值选股之FFScore模型
【华泰金工林晓明团队】相对市盈率选股模型A股市场实证研究
【华泰金工林晓明团队】华泰价值选股之现金流因子研究——现金流因子选股策略实证研究
【华泰金工林晓明团队】华泰基本面选股之低市收率模型——小费雪选股法 A 股实证研究
【华泰金工林晓明团队】华泰基本面选股之高股息率模型之奥轩尼斯选股法A股实证研究
基金定投
【华泰金工林晓明团队】大成旗下基金2018定投策略研究
【华泰金工林晓明团队】布林带与股息率择时定投模型——基金定投系列专题研究报告之四
【华泰金工林晓明团队】基金定投3—马科维茨有效性检验
【华泰金工林晓明团队】基金定投2—投资标的与时机的选择方法
【华泰金工林晓明团队】基金定投1—分析方法与理论基础


