【国盛量化】BL模型的泛化扩展：熵池模型之理论篇 | 量化专题报告

来源：留富兵法

报告摘要

本报告将介绍一种前沿观点融合模型：熵池模型。熵池模型由KKR前首席风险官Attilio Meucci于2008年提出，主要作用为将主观或者量化的观点通过分布更新的形式融入到风险模型中，用于资产配置或资产定价。模型当前在许多海外的大型金融机构中已开始普及。

熵池模型vs BL模型：泛化能力与调整精度的双重提升。BL模型作为观点融合的创立者已经越来越难适应当前资产配置和风险管理需求。熵池模型相比BL模型在风险因子选择、观点表达对象、观点表达形式、观点相关性等方面进行了全方位扩展，几乎可以在任意分布下，对于任意对象，表达线性或非线性的任意观点。其通过最小化相对熵和池化的算法能够对风险因子联合分布进行全局的调整，理论上更为精确合理。

熵池模型背后的统计学思想：最大熵原理。信息与系统的熵数量相等，方向相反，信息的作用就是减熵。然而在观点约束下选择的后验分布应当是不确定性最强的，增加冗余结构最少的分布，不应使用观点约束以外的信息进行过度减熵，是谓“最大熵原理”。熵池模型通过最小化相对熵求后验分布，本质是以最大熵原理避免不必要的假设和结构，防止主观臆断风险。

利用熵池模型实现观点逻辑与量化模型的有机结合。本报告通过资产配置实例发现，熵池模型对于预测信号的利用率更高，产生的后验分布对于未来更有预测性，策略的年化收益与夏普率都有显著提升。在预测信号精度和广度的不断提升下，通过熵池模型可以给资产配置模型提供更多的Alpha。除了资产配置，熵池模型在压力测试、因子择时、行业配置、衍生品定价、衍生品做市等问题中，都具有应用前景，我们认为未来其终将成为主流的观点融合模型。

一、什么是熵池（Entropy Pooling）模型

1.1. 完全自由观点

在资产配置领域，均值方差模型虽然在数学上十分优雅，但它在投资实务中并不能直接使用。这是因为它给出的最佳投资组合对该模型的核心输入即资产的期望收益率非常敏感，而期望收益率很难准确预测，往往需要靠多个模型多位专家提供更多的判断来提高精度，均值方差模型缺少一个观点融合的模块。

为解决这个问题，高盛的Fischer Black和Robert Litterman在1992年提出了后来业界闻名的Black-Litterman模型（以下简称BL模型）。该模型以市场均衡假设反推出的资产收益率为出发点，结合投资者对不同资产收益率的主观判断，最终通过贝叶斯收缩估计的方式确定资产的收益率分布，并计算最佳的投资组合配置。这为之前仅通过历史估计来确定资产收益率分布的方式拓展了进步空间。

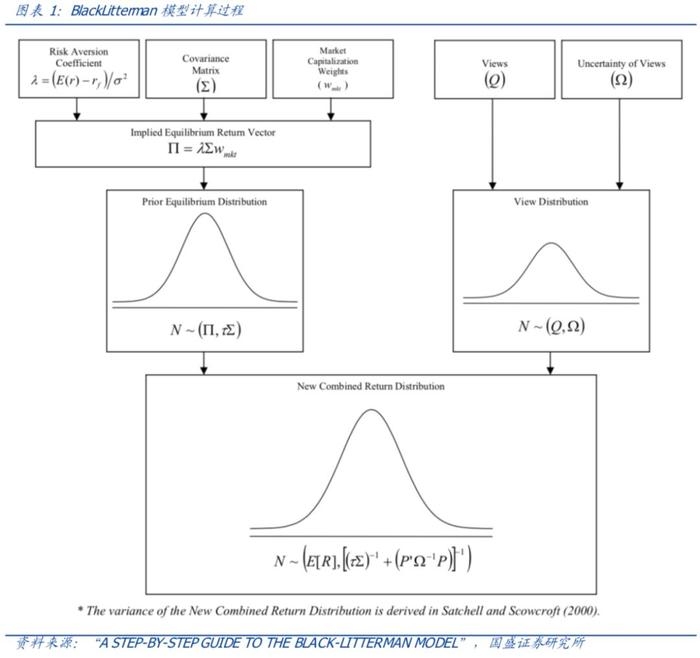
虽然BL模型已然能够通过贝叶斯方法将相应的资产绝对收益和相对收益观点融入到所估计的均值方差中，但是观点的灵活性较弱，必须为确定的收益率期望观点。对于收益率中位数、收益率范围、收益率排序、波动率、相关性、尾部分布、非线性特征等等观点BL模型无法融合，而实际投资过程中产生的观点有很多都是诸如判定方向或者大致区间的形式，同时对波动率、相关性等的判断也有很大的意义。除此之外BL模型是在正态分布的框架下的，而我们知道正态分布仅是一种便于计算的近似，与实际分布的尖峰厚尾有偏特性有较大差别，容易导致对尾部风险的欠估计。

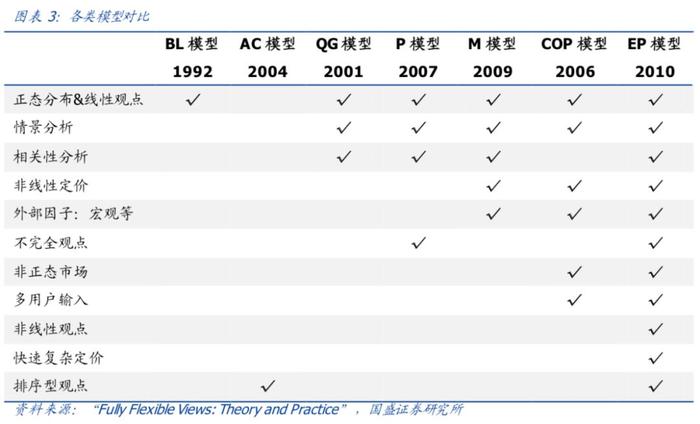
针对BL模型的问题，众多学者提出了相应的解决方案：Edward Qian、Stephen Gorman在2001年提出了新的模型（以下简称QG模型），将针对波动率和相关性的观点设计到了模型中，Robert Almgren、Neil Chriss在2004年提出了将收益率排序观点进行融合的模型（以下简称AC模型），Jacques Pezier在2007年提出了在最小区别原则（Least discrimination）下的相对熵模型（以下简称P模型），而本报告将介绍由前KKR首席风险官Attilio Meucci提出的熵池（Entropy Pooling）模型（以下简称EP模型），EP模型以简洁优雅的设计解决了上述模型提到的所有问题，能够融入几乎任何形式的观点，同时先验分布可以是任意分布，计算方便快捷，可谓集大成者。Attilio Meucci之前在2006年和2009年也分别提出过另外两个模型（以下简称COP模型和M模型）对部分问题进行过探讨，相应文献详见文末。

1.2. 贝叶斯更新的一般化

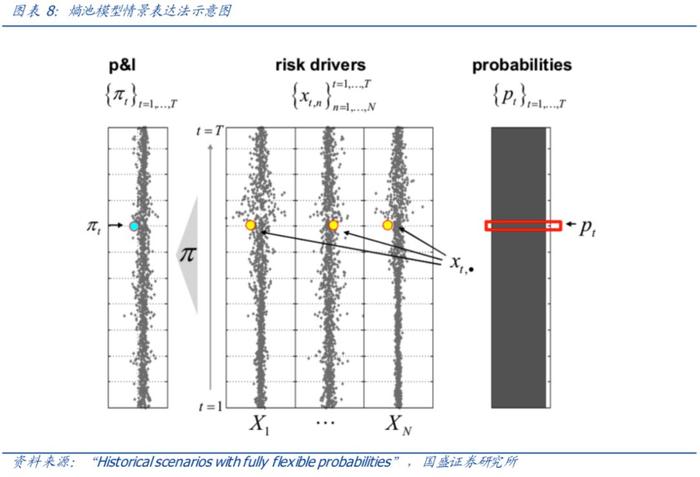
EP模型所考察的对象并不局限于资产的收益率分布，而是泛化成任意风险因子的分布。假设一组证券由N维的风险因子X决定，那么必然存在一个确定性的函数P将风险因子X与当前可得的信息I_t映射到每个证券未来的价格P_(t+τ)。

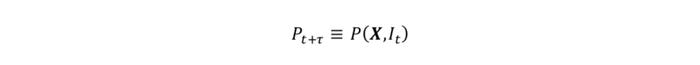
比如假设这组证券是期权，风险因子X代表了所有标的资产的价格和隐含波动率变化，那么函数P就可表示为一个由“deltas”、 “vegas”、 “gammas”、 “vannas”、 “volgas”等等系数组成的二阶泰勒展开式。X也可以包含和证券价格仅有统计相关性的外部变量（包括宏观因子等）。总之，EP模型当中的X并不局限于资产的收益率。

在此基础上，首先假设存在一个类似BL模型中先验分布的参考模型。所谓的参考模型就是风险因子X的先验联合分布，可以用概率密度函数来表示：

而我们需要解决的问题即为最优化证券的权重配置，使得在投资限制C下满意度函数S最大化。满意度函数S可以理解为由投资者所确定的效用函数：

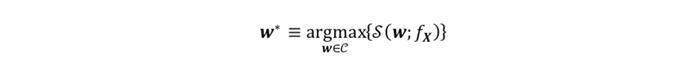
EP模型最重要的泛化扩展在于投资者观点可以表达在风险因子X的一组广义函数上：g_1 (X),…,g_K (X)，而不仅仅是风险因子上。这些广义函数并不一定需要线性，投资者甚至可以直接在证券定价函数g_i (X)=P(X,I_t )上表达观点。这些广义函数组成了一个K维的随机向量V，其先验联合分布可由参考模型计算得到：

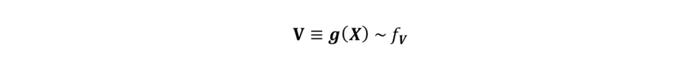
当然所谓的观点一定是不同于参考模型的，因而在V上表达的观点会使得V服从一个由观点更新后的分布：

对两个分布包含的结构进行量化，EP模型采用了信息论中的香农熵：

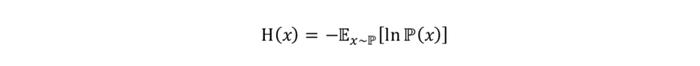
对于两个分布的差异，EP模型采用相对熵即KL散度（Kullback-Leibler divergence）进行描述，从而后验分布即为在满足投资者观点下与参考模型结构最为接近的分布：

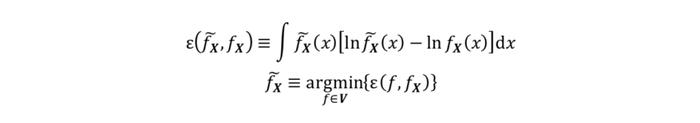
公式中的f∈V代表了满足投资者观点的所有分布。最后类似BL模型，投资者对观点的信心需要体现在后验分布中，假设投资者对其观点持100%的信心，那么后验分布就是上式求的的分布，否则的话后验分布需要向参考模型收缩：

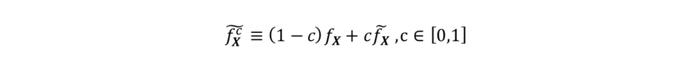
若存在着多个不同信心的观点，也可通过对100%信心的后验分布进行信心加权的方式进行融合，比如假设有S名专家分别对各自的g(X)输入了他们的观点，那么我们可以得到S个100%信心后验分布。最终后验分布即为：

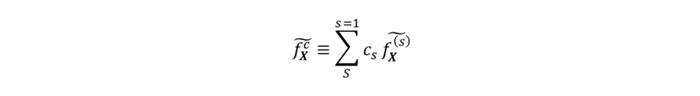
此过程被称为“观点池化”（Opinion-Pooling），因此EP模型概括的来说就是将以相对参考模型熵最小的后验分布（观点）汇集的模型。“Pooling”一般翻译为“池化”，但其意义更接近于“汇集”。

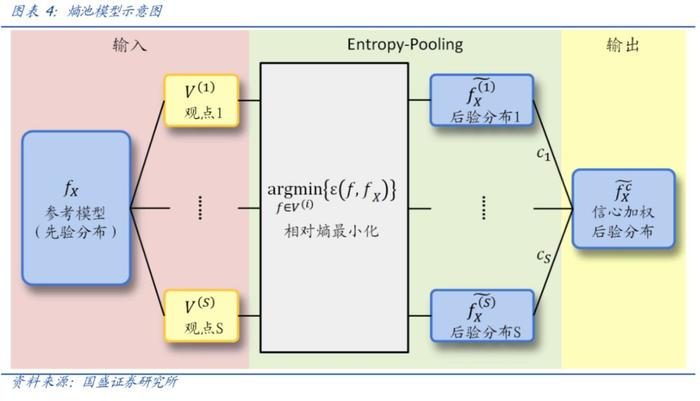
从模型的输入输出来看，模型本质是通过观点信息更新了分布，与BL模型作用相同，但是相对熵最小化更新的方法相比贝叶斯更新更为一般化。在Ariel Caticha与Adom Giffin在2006年的论文“Updating Probabilities”中证明了贝叶斯更新只是相对熵最小化更新的一种特殊形式，两种方法是相洽的。如今相对熵最小化的方法已经被应用到了除传统热力学、信息论以外的各个领域，特别是机器学习和金融工程。

1.3. 相对熵最小化的意义

为了便于读者直观理解，本报告在此简单阐述为什么要用熵来度量一个分布的结构。在信息论中，熵的本质是一个宏观态所对应的微观态的不确定性。举一个简单例子来说明，掷三次硬币可能出现三次都是正面，也可能出现一正二反，三次都是正面的可能性只有一种，而一正二反的可能性有三种：正反反、反正反、反反正，因此这里一正二反这个宏观态的熵（微观态不确定性）要高于三次正面。

对于熵的度量，可以以抛硬币这样的二元等概率事件作为参照物来计算，如果某一宏观态对应8个微观态，那么这相当于抛掷三次硬币产生的可能微观态2^3=8，因此计算上可以用对数来度量熵：3=log2(⁡8)，单位为比特（bit）。当然度量熵的底数也可以是自然常数e，此时熵的单位被称作纳特（nat）。对于一个完整的分布，可以通过将分布中每个宏观态的熵按照概率加权得到分布的熵，这就是香农熵的概念。

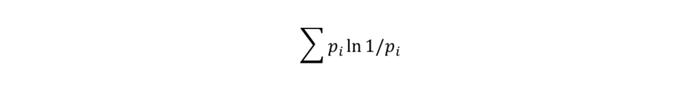
一个100%可能的宏观态熵为0，而多个宏观态均匀分布的熵最大，其余分布介于两者之间。所以确定性越高的分布熵越小，当一个分布仅指向一个宏观态时，这个分布蕴含了需要了解这个系统的所有信息，不再需要获取别的信息来对系统减熵。举个简单的例子：如果我们知道所有的投资者明天的所有操作，那么明天股市的涨跌就是确定的，否则只能用一个不确定的概率分布来描述，信息越多此概率分布的确定性越强熵越小。信息（正确的观点）与熵数量相等，方向相反，信息的作用就是减熵。

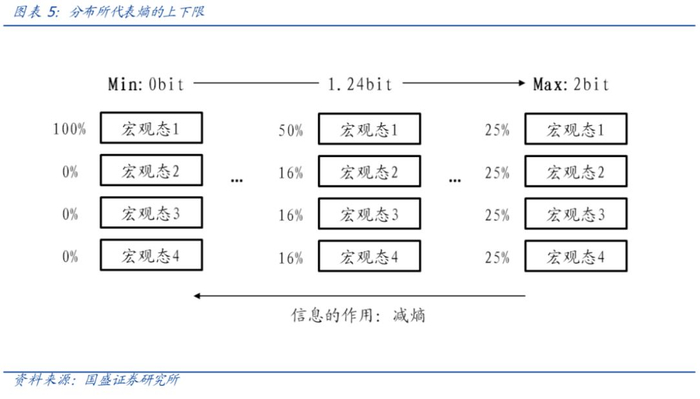
而EP模型提出的相对熵最小化本质就是在观点约束下选择增加多余信息最少的后验分布，其遵循的是“最大熵原理”。最大熵原理是1957年由美国统计学家、物理学家E.T.Jaynes提出的，观点将带来新的信息量，因而后验分布的熵一定小于先验分布，而满足观点约束的后验分布有无穷多个，“最大熵原理”是指在这些分布中选择熵最大，最具有不确定性的那一个，尽量不加入多余假设和结构。就像上图的例子中，在四个宏观态均匀分布下，如果我给出“宏观态1有一半概率是真的”的观点后，其余三个宏观态最好保持均匀分布，而不是主观的给予额外的结构。

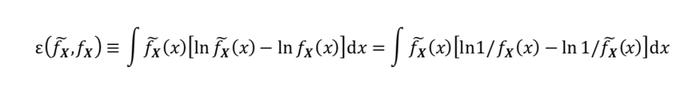
1.4. 模型解析解与数值求解

模型在正态分布下具有和BL模型类似的解析解，具体详见报告。

如果分布并非正态或者观点的形式更为复杂，则EP模型难以获得解析解，所幸的是EP模型的数值解法非常简洁，大部分情况下仅涉及到线性约束（也可以非线性）下的优化问题，计算十分方便快速，对延迟要求较高的交易模型或者极为复杂的定价模型有着独特的优势。这也是EP模型的另一个优雅的地方。具体详见报告。

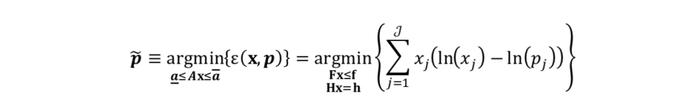
二、熵池模型 vs BlackLitterman模型

2.1. 观点融合

EP模型相对BL模型的第一大优势就在于观点融合的泛化。BL模型只能对于资产未来期望收益率发表等式约束的观点，但是EP模型不仅观点的对象更泛化，观点的表达方式也更泛化：

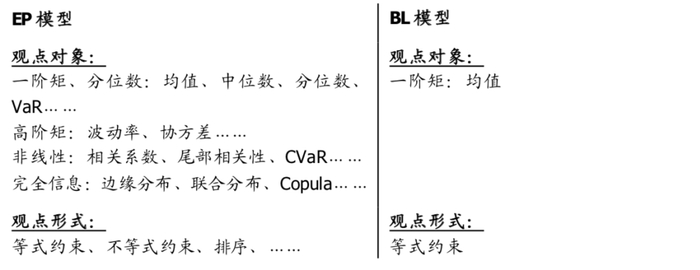
各类观点表达细节详见报告。

2.2. 信心水平

BL模型主要通过刻度系数τ和信心矩阵Ω来确定具体观点信心水平。有关BL模型的这两个参数的确定我们例举文献如下：

1、“Global portfolio optimization” Black F, Litterman R. , 1992

在Black和Litterman的原始报告中，他们认为τΣ刻画了资产均衡收益均值的不确定性，它是正比于资产均衡收益协方差矩阵的Σ，而由于收益均值的不确定性远远小于收益观点的不确定性，因此他们认为τ应当相当接近于0；

2、“Using the Black-Litterman Global Asset Allocation Model” Bevan and Winkelmann，1998

在这篇报告中，作者认为信息比率IR可以衡量主观观点所包含的信息量，他们认为从统计意义上来说，超过2的IR代表了超额收益达到了2倍的标准差之外，因此是很难发生的，所以τ的设置应该使得IR小于2，使得最后得到的权重不会过于极端。

3、“The Intuition Behind Black-Litterman Model” He and Litterman, 1999

在这篇报告中，作者认为τ应该与观点信心矩阵Ω结合来设置，可以首先假定一个τ，然后校准观点的信心水平，使得ω_k/τ=p_k'Σp_k。这样的设置下τ的值并不关键，关键在于比率ω_k/τ，只要比率确定了不论τ为何值，后验的预期收益向量不变。

4、“A demystification of the Black–Litterman model: Managing quantitative and traditional portfolio construction” Satchell and Scowcroft, 2000

在这篇报告中，作者认为τ是刻度因子，因此经常设定为1。观点的权重完全由观点信心矩阵Ω来确定。

5、“A STEP-BY-STEP GUIDE TO THE BLACK-LITTERMAN MODEL” Idzorek, 2002

这是较为经典的一篇报告，在He and Litterman（1999）的基础上，作者认为观点信心除了p_k'Σp_k还受到其他因素的影响。作者提出了一种可以结合直观的0%-100%的主观信心的参数确定法。在此参数确定法下τ是一个无关紧要的标量，在设定完τ之后可以在此基础上设置Ω，τ的大小不影响最终计算的后验预期收益率向量。此方法涉及复杂的计算和优化。

以上论文仅是讨论刻度系数τ和信心矩阵Ω的部分论文，从这部分论文中我们已经可以看出BL模型在信心水平确定上的不直观性和参数关系间的复杂性，学术界对其的争论也较多且并未统一。从实证角度来说，由于观点融合模型的回测建立在观点模型和配置模型的基础上，各家在说明各自方法的时候并不是建立在一个公认的观点模型和配置模型的基础上，因而更加难以互相说服。相比BL模型，EP模型在信心水平的确定上更为直观，我们可以用信心水平直接对各个观点集给出的后验分布进行加权。

EP模型中的信心水平可以设置为观点在历史上的胜率，或者也可以类比采用Grinold和Kahn在《主动投资组合管理》中提到的主动管理基本定律的方式：

其中IC即历史观点与实际情况的相关系数，而Breath就是历史产生过的观点数。如果有多个信心不同的观点，可以通过“机制转换（Regime Switch）”的方式理解加权后的分布，并通过“幂集”映射，可以将观点的相关性加入模型（具体详见报告）。这又是EP模型相对BL模型的一个优势。BL模型的观点信心矩阵Ω是对角阵，是不考虑观点之间的相关性的，一旦需要考虑到观点之间的相关性，从而给观点信心矩阵Ω的非对角线元素赋值，将又是一个难题。而EP模型在历史观点频率相同的情况下，可以直接按照几个观点是否同时正确的情况给相应幂集赋予概率即可，非常直观。

2.3. 解析解对比

在不考虑信心水平的情况下，即假设各观点的信心都相同且为100%时，那么BL模型和EP模型的解析解分别可以表达为如下形式：

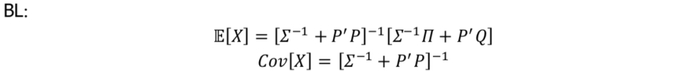
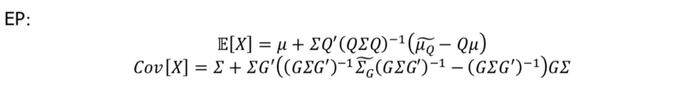
从公式中可以看出，在BL模型中只要表达了观点，不论观点与先验分布是否一致，都会使得协方差矩阵中相应的资产波动率减小，也就是说不确定性下降。但是如果观点与先验分布一致，本质代表的是观点并未带来任何减熵的信息，从而分布不应该变化，资产的波动率也不应减小。而在EP模型中，如果观点与先验分布一致，后验分布就等于先验分布，不会有变化。因此从这个角度来说，EP模型也比BL模型更加合理。

三、熵池模型的应用实例

3.1. 资产配置场景下的熵池模型优点

熵池模型主要解决观点融合问题，在整体资产配置框架中起到承上启下的作用。在观点融合问题解决后，不断拓展观点端各类模型（客观亦或主观）的预测精度和预测广度，将给资产配置带来源源不断的正向作用，好比Alpha端之于选股模型。

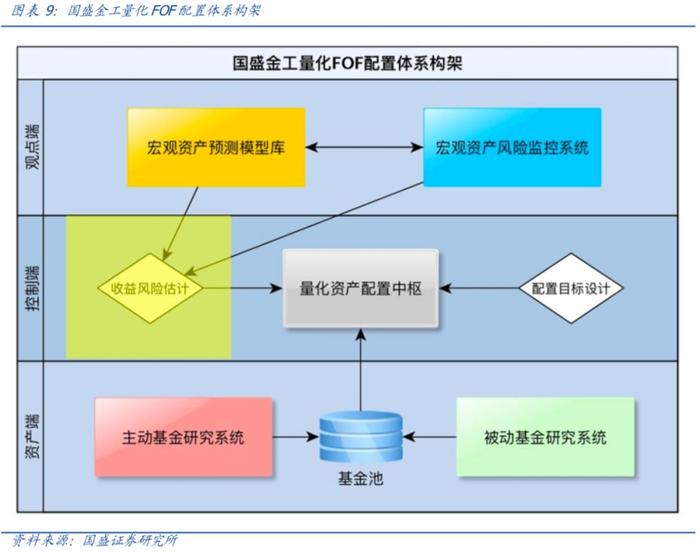
在我们之前的报告《宏观逻辑的量化验证：中国利率先行指标体系构建》当中，我们通过简单分布平移的方式融合新观点，其主要过程为：

1、将利率预测的信号通过久期公式转化为国债收益率期望E_预期 (X_国债 )；

2、将每一个国债历史收益率加上均值调整项：E_预期 (X_国债 )-E_历史 (X_国债 )。

经过此调整后的国债收益率分布均值将变为利率模型预测下的均值，从而为资产配置模型带来一定的Alpha。这样调整的好处在于不会改变国债收益率分布的方差、偏度、峰度等高阶矩特征，使得其边缘分布形状不变。而这样的调整也有坏处：

1、分布平移使得尾部发生了变化，比如预测均值高于历史均值，则会导致左尾减小（最坏情况变好），风险被低估，预测目标（均值）与最终调整结果（均值+尾部）不匹配；

2、简单分布平移仅针对所预测的资产，对于与其有相关性的资产无法同时调整，比如当股债同步时，提高债券的收益率均值理论上应同样提高股票收益率均值，如果没有相应的外部股票模型发出观点，简单分布平移难以对股票作出合适调整。

而熵池模型则不存在这两个问题，首先EP模型情景集不变，因此后验分布中尾部范围不会变化，仅是尾部发生的概率可能被调整。而针对第二个问题，我们以一个数值实验来说明。首先构造两个均值皆为0的资产收益率分布，其相关系数设为0.6。针对第一个资产给予观点：

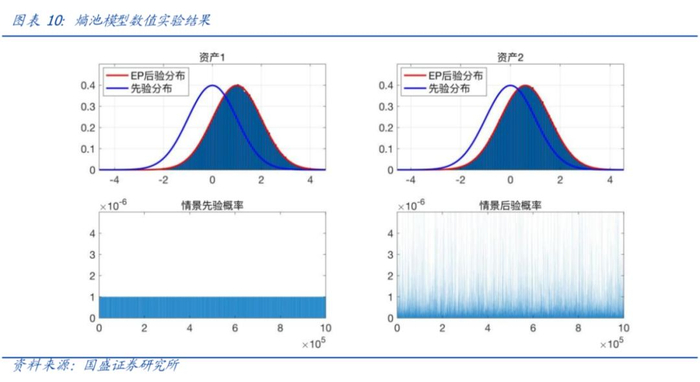
通过EP模型计算后得到的后验分布中资产1的均值达到了观点的要求为1，而资产2的均值达到了0.6。也就是说EP模型能自动根据相关性调整所有资产的分布，当一个资产的均值被调高后，与其正相关的其他资产均值也会被适当调高。在整体资产分布较为复杂，观点多样化的情形下，EP模型以最大熵原理对分布进行整体的调整，比简单分布平移或者主观臆断调整更为科学便捷。

3.2. 熵池模型下观点融合的实际效果

在本报告中，我们继续沿用《宏观逻辑的量化验证：中国利率先行指标体系构建》中的资产配置模型：概率优化模型，以及10年期国债收益率预测模型。选用如下资产进行资产配置模拟测试：

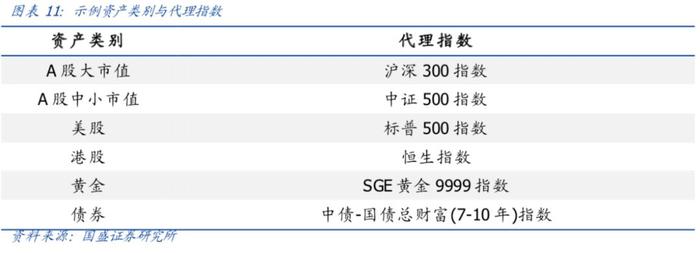
我们将优化函数设置为以下风险目标：考虑双边0.5%的换手费用下，未来1个月收益小于1%或者最大回撤超过-0.6%的概率。并通过蒙特卡洛优化算法以月频为调仓周期最小化此风险目标以求出最优的资产配置比例。

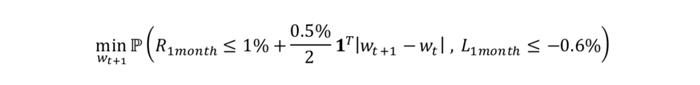
对于输入的资产收益率分布，我们分别采用历史分布、简单平移分布和EP完全信心分布进行回测，后两者将利用同样的利率预测信号调整历史分布。所输入的10年期国债收益率预测信号的历史月度方向胜率为69%，信号通过与中债-国债总财富(7-10年)指数的历史久期的组合即可计算出其未来预期收益率。

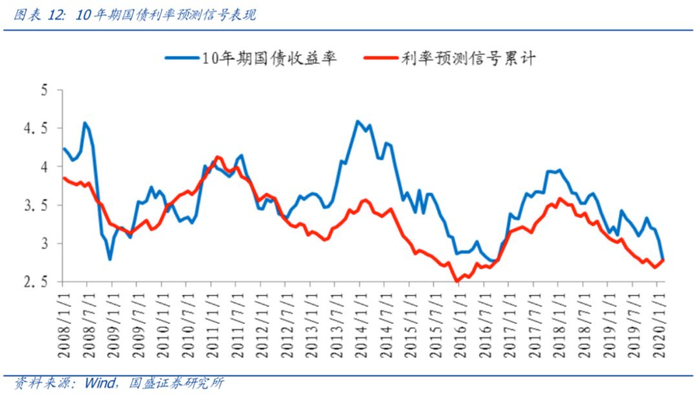
模型2008年1月至2020年1月回测结果如下：

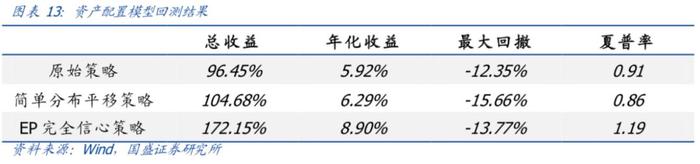
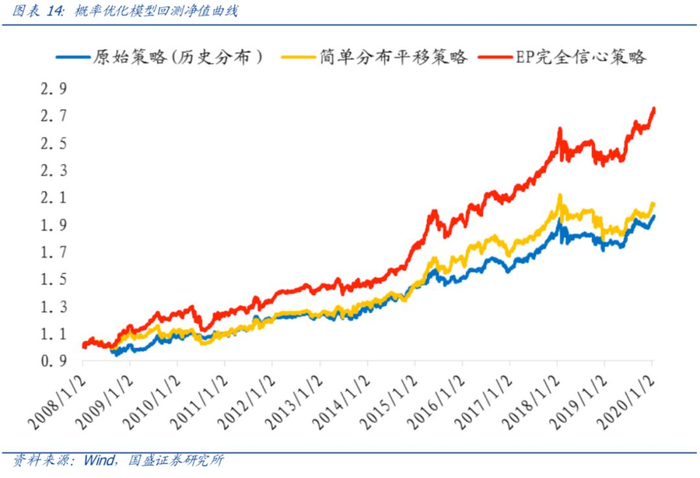
从回测结果来看，EP模型对利率预测信号的利用效果远远好于简单分布平移，简单分布平移中的许多看似细枝末节的问题对最终的配置结果造成了很大的影响。EP模型利用利率预测信号通过最大熵原理对整体分布进行全局的调整，使得后验分布对未来更具有预测能力。

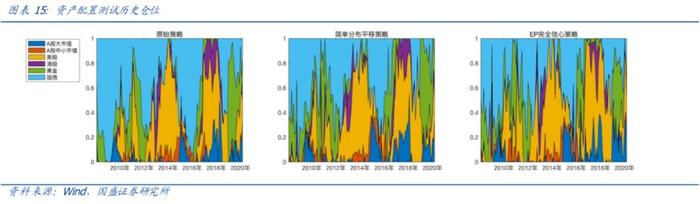
四、总结与展望

4.1. 熵池模型的优点总结

EP模型在解决观点融合和分布更新的场景下，其无论是从泛化能力还是从调整精度来说都要优于传统方法，当前已有瑞典北欧斯安银行（SEB，北欧最大的金融集团之一）、安本标准（Aberdeen Standard，英国最大的主动式资产管理公司）等机构开始使用。相关论文也在2010年以后不断有发表，对模型进行不断的测试与修正，因此本报告希望国内也能有更多机构投资者了解到此模型，并在投资实践中受益。熵池模型的最主要的优点可以归纳为如下几点：

1、可融合几乎任意形式的观点（线性与非线性、等式与非等式）；

2、可对任意分布进行观点融合；

3、可以幂集映射的方式融入观点间的相关性；

4、观点的影响具有整体性，会对相关资产做全局调整；

5、利用最大熵原理避免不必要的假设和结构；

6、情景表达法下无需重定价，计算速度更快。

4.2. 熵池模型拓展与应用场景展望

当资产配置研究达到一定程度后，自然而然需要将观点逻辑与量化模型进行有机的结合。以安本标准为例，其在大类资产判断上构建了许多的情景，他们认为资产收益率之所以有肥尾特性，主要是因为市场并不只有一种状态，通过分析市场的不同状态，构建出未来可能的情景，就可以对资产组合进行压力测试，这将有助于提高资产配置的稳健性和应对风险的能力。其中，熵池模型就扮演着观点逻辑与风险模型有机结合的角色。因此，对于熵池模型，我们未来的一个展望就在于可以应用在压力测试上。

关于熵池模型本身，其实仍有较多的扩展空间，首先其应用的范围不局限于资产配置场景，对于因子择时、行业配置、衍生品定价、衍生品做市等，都具有应用前景，在今后的报告中，我们将对其中的部分场景展开研究。熵池模型从理论层面也有扩展空间，包括极端观点的融合、路径分布代替样本点的分布、因子模型下的表达等值得我们未来去探索。

参考文献

[1] Almgren, R., & Chriss, N. (2007). Optimal portfolios from ordering information. In Forecasting Expected Returns in the Financial Markets (pp. 55-100). Academic Press.

[2] Bevan, A., & Winkelmann, K. (1998). Using the Black-Litterman Global Asset Allocation Model. Goldman Sachs.

[3] Black, F., & Litterman, R. (1992). Global portfolio optimization. Financial analysts journal, 48(5), 28-43.

[4] Caticha, A., & Giffin, A. (2006, November). Updating probabilities. In AIP Conference Proceedings (Vol. 872, No. 1, pp. 31-42). American Institute of Physics.

[5] He, G., & Litterman, R. (2002). The intuition behind Black-Litterman model portfolios. Available at SSRN 334304.

[6] Idzorek, T. (2007). A step-by-step guide to the Black-Litterman model: Incorporating user-specified confidence levels. In Forecasting expected returns in the financial markets (pp. 17-38). Academic Press.

[7] Meucci, A. (2008). Fully flexible views: Theory and practice. Fully Flexible Views: Theory and Practice, Risk, 21(10), 97-102.

[8] Meucci, A. (2010). Historical scenarios with fully flexible probabilities. GARP Risk Professional, 47-51.

[9] Pezier, J. (2007). Global portfolio optimization revisited: A least discrimination alternative to Black-Litterman (No. icma-dp2007-07). Henley Business School, Reading University.

[10] Qian, E., & Gorman, S. (2001). Conditional distribution in portfolio theory. Financial Analysts Journal, 57(2), 44-51.

[11] Satchell, S., & Scowcroft, A. (2000). A demystification of the Black–Litterman model: Managing quantitative and traditional portfolio construction. Journal of Asset Management, 1(2), 138-150.

风险提示：量化模型结果基于输入数据，如若输入数据不具有预测性，不保证模型的样本外效果。

本文节选自国盛证券研究所已于2020年03月18日发布的报告《BL模型的泛化扩展：熵池模型之理论篇》，具体内容请详见相关报告。