来源:XYQUANT
导读
1、多因子选股体系中不可规避的一个问题是因子选择,该领域的学术以及商业研究相对较少。作为机器学习系列二研究,我们通过引入机器学习中的特征选择方法,运用Filter&Wrapper构建因子选择体系,进一步构建线性和非线性融合的动态选股因子,该因子选股能力斐然。
2、针对于选择的因子通过线性回归的方式构建动态选股因子DLS:因子IC、ICIR、T值分别为0.106、1.50、16.06,而基准(选择过去5年ICIR最优 因子等权合成)则分别为0.061、1.16、12.48;分位数测试来看,DLS因子多空年化收益、夏普率分别达到43.0%、4.99,同期基准达到24.3%,3.48,且DLS因子在各组别中的单调性和稳定性要优于基准的表现。
3、为了更好的利用非线性选股信息,我们将机器学习系列一构建的集成学习因子引入到线性回归中(相当于在Filter&Wrapper选择的因子基础上添加集成学习因子),构建线性和非线性叠加的A-DLS因子。A-DLS因子IC达到0.13、ICIR为2.07,多空组合年化收益69%、夏普率6.55,整体表现优于集成学习因子。
4、基于A-DLS 因子构建主动量化以及增强选股策略,各策略表现优异。其中主动量化策略年化超额收益26.9%、夏普率4.61;针对于沪深300和中证500采用线性优化的方式构建指数增强策略,以针对于中证500构建的全市场选股增强策略为例:策略超额收益达到18.4%、风险收益比达到4.14、最大回撤3.7%。
风险提示:文献中的结果均由相应作者通过历史数据统计、建模和测算完成,在政策、市场环境发生变化时模型存在失效的风险。
一、引言
1.1
效用递减、进退两难
1952年Markowitz建立了以均值方差模型为基础的现代资产组合管理理论(MPT),该理论确立了金融学收益风险均衡的分析范式,标志着现代金融学的诞生。Black、Sholes 和 Morton 于1973年建立了期权定价模型(OPM),为衍生品定价问题确立了分析范式;Ross在1976年建立了无套利定价理论(APT),构成量化选股的理论基础;进一步Fama与其同事French在1992年提出了Fama-French三因子模型。至此,现代量化投资的理论基础的构建大致完成。
在量化理念从混沌初开到如今枝繁叶茂的漫长征途中,出现过因子选股、统计套利、趋势交易等著名的投资模型,也出现过LTCM、文艺复兴、AQR等量化巨头公司……但当下不少国内的量化投资从业者却正在面临着越来越激烈的竞争和不断衰退的阿尔法(超额收益)。以量化选股领域为例:1、曾经选股能力强的因子的有效性在不断降低,且波动愈发剧烈;2、以往的数据源、研究视角/研究方法进一步挖掘的边际效用不断递减,投入产出比在持续收窄;3、随着模型和数据同质化的加剧,踩踏风险也变得越来越高。该如何有效的应对这些问题是每个量化从业者面临的难题。
实际上面对上述挑战,已经有业界人士给出了一些值得尝试的方案:为了应对日渐波动的市场和不断切换的风格,可以考虑将动态因子选择机制常态化;为了应对日益丰富的数据来源和越来越大的数据量,可以采用机器学习/人工智能的方法去提升处理数据、探索规律的效率;为了解决传统的静态模型的弊端(1、对非线性规律把握难度较大;2、因子和权重设置相对固定,很难适应国内市场快速切换的现实情况;3、静态模型的搭建需要大量的历史数据做回测以大概率地保证因子的长期有效性),我们可以构建动态选股模型……
正如所有新事物的诞生、成长都需要一个过程,这些新的方法也面临着诸多挑战。质疑者认为:动态因子选择长期来看不够稳定,同时也增加了交易的成本;机器学习方法过于复杂、难以解释、黑箱属性较重;动态模型主要依靠数据驱动,模型的逻辑性和样本外表现都有待于进一步商榷……但无论怎样,正是这些质疑的声音构成了我们前进的动力,也正是这些质疑让量化选股体系变得更加完善。我们有理由相信这些新的方法经过不断的打磨和雕琢,终将成为未来量化选股模型的中流砥柱。届时我们亦不必进退两难,正应了那句话:前途是光明的、道路是坎坷的、尝试是值得褒奖的。
兴业证券金融工程团队将机器学习应用于量化选股体系的研究正是在这样的背景下产生的。我们并不会简单地将每一个机器学习算法都做一些尝试(实际上在2015年-2016年我们有撰写过5篇机器学习的深度报告,详细介绍了各种算法在选股领域的应用),而是更加看重基于某个具体角度的深入挖掘,注重研究的延展性和可落地性。继上一篇《基于集成学习算法的量化选股模型研究》在2019年6月发布之后,我们推出了机器学习系列的第二篇深度报告《当线性遇上非线性》。本系列的第一篇报告以改进版的Adaboost算法为核心,将非线性信息利用、因子动态选择、因子权重确定等一系列问题有效地融合于同一个分类算法之中,取得了非常好的实践效果;而本文则将目光聚焦于更为传统、却也更受主流投资者喜爱的线性多因子体系,并主要在以下两个方面有所突破:
1.借鉴机器学习中Filter&Wrapper的特征选择方法,构建了一套系统化的、有效的动态因子选择机制;
2.引入我们之前开发的集成学习因子E-NELS,将其视作因子对股票收益非线性预测能力的代表,而后将该因子纳入我们的线性模型框架,构建线性、非线性彼此融合的新一代多因子框架。
在正式介绍模型之前,我们先将本文的研究测试时段做一个说明:整个研究样本的时段为2005年1月4日-2019年7月31日;如不加特殊说明,我们一般采取60个月的滚动窗口的实证方式,因此因子和策略的样本外研究自2009年12月31日开始。
二、机器学习之因子选择综述
2.1
机器学习简介
在《基于集成学习算法的量化选股模型研究》的深度报告中,我们详细的对机器学习的大致分类、算法、集成学习的方法等做了详细介绍,并对人工智能/机器学习在投资领域的应用做了简单描述。整体来看机器学习在量化领域的应用越来越广。
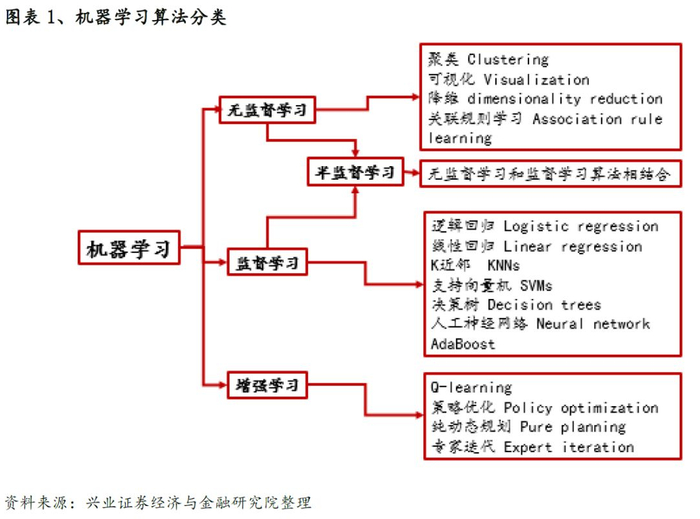

人工智能、机器学习对投资的影响应该说是全流程的,从新数据源的解析与挖掘,到模型构建的方方面面,再到具体的交易模块,越来越多的业界投研人员将两者紧密地结合在一起。具体到我们平日常用的线性多因子框架,其中的因子选择环节就是一个展现机器学习方法优势的非常好的例子。
我们知道多因子体系的基石是大量的选股因子。一般来说,选股因子可以分成以下几个大类,包括:价值、成长、质量、动量/反转、分析师情绪、另类(技术、规模、流动性、风险)等。构建每类因子所需的信息不同,因子选股的表现也是千差万别,而且因子之间(同类或不同类)也存在着或多或少的相关性。因此,如何从已有的因子库中有效地进行因子选择,就成为了每个模型都必须解决的问题。在传统的线性模型中,普遍的做法是根据每个因子的中长期表现,选择具有一定选股能力且符合经济逻辑的因子。这种方法的好处是简单易行,且能够与管理人的主观判断相符,但其缺陷也是显而易见的:筛选过程过于主观、不可复制,容易利用到未来数据,在因子数量较多时效率极低且缺乏一个系统性地应对市场变化的机制。为了解决上述问题,我们将目光转向机器学习的王国,尝试从特征选择和特征提取的角度寻找解决因子动态选择问题的方法。那么,到底什么是特征选择和特征提取呢?
2.2
特征选择与特征提取
在机器学习中,随着数据维度的上升,提供可靠分析所需的数据量将成倍增长。贝尔曼将这种现象称为“维度的诅咒【1】。
当数据集的维数持续增加时,数据集中有意义的数据将会越来越稀疏,这将增加证明模型结果具有统计学意义的难度。而大数据集中所谓的“大𝑝,小𝑛“问题(其中𝑝是特征数量,𝑛是样本数量)往往使模型过度拟合,从而将小波动误认为是重要的数据差异而导致分类错误。此外过多的特征也会使得数据集的噪声增加,数据集中的噪声定义为“测量方差的误差”,可能来自测量误差或数据本身的方差【2】。机器学习算法很容易受到嘈杂数据的影响,另外从计算量上来看,随着维度的增加计算成本也会以指数方式提升,因此应该尽可能的减少噪音以避免不必要的复杂性,从而提高算法的效率【3】。
要克服以上问题就必须要找到一种方法来减少备选的特征数量。解决高维数据集问题的一种流行方法是从原始数据集中挑选出有效的变量,删除无效的变量。或者在尽可能保留信息的条件下,寻找一种映射方法将高维数据投影到低维空间上,这两种技术分别称为:特征选择(feature selection)和特征提取(feature extraction)。
2.2.1 特征提取
特征提取通过组合原始变量创建新变量,从而减少所选特征的维数。特征提取算法有两大类:线性和非线性。
线性特征提取假设数据位于较低维度的线性子空间,从而可以直接通过矩阵分解将数据投影在子空间上以实现降维。常见的方法有PCA-主成分分析【18】,ICA-独立成分分析【19】及MDS【20】。非线性特征则通过不同方式进行降维,常见的方法有两大类:1、针对特征之间的非线性关系,可以使用提升函数将特征映射到更高维空间。在更高的空间上,特征之间的关系可以被视为线性的,从而我们能使用线性降维的方法,将高维数据映射回较低维度的空间以实现降维。常见的方法有Kernel PCA【21】;2、另一种方法通称为流形学习Manifold Learning【22-25】,其思想是若高维数据存在流形结构,则我们能通过非线性方法将高维数据映射到低维空间,同时尽量保有高维数据的本质。
常见的特征提取方法总结如下:
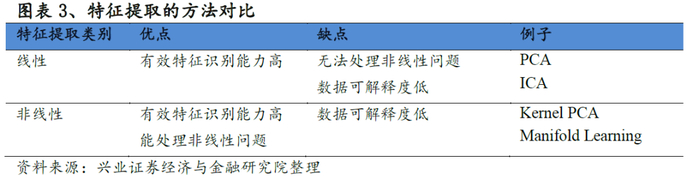
2.2.2 特征选择
与特征提取方法不同,特征选择技术不会改变原始数据的表现形式【4】,该技术是通过删除不相关或多余的特征从而达到降维,实现方法分为三类【5-6】:
1.过滤式特征选择,直接从数据中提取特征(与后续学习过程无关);
2.包裹式特征选择,把最终将要使用的模型性能作为特征子集的评价准则;
3.嵌入式特征选择,将特征选择过程与学习器训练过程融为一体,两者在同一个过程中完成。
过滤式(Filter)
过滤式方法使用模型效能以外的度量来确定该特征是否有用。该方法通过描述性指标对特征进行排序筛选,而不是以所使用的模型(如包装方法中的模型)的拟合效果来选择特征子集。过滤方法的优点是计算时间非常短、不存在过拟合问题。然而,该方法忽略了特征之间的任何交互或关联。常见的三种不同过滤方法是方差分析【7】、皮尔逊相关分析【8】和信息增益分析【9】。
方差分析(ANOVA, Analysis of variance) 的思路为:按照不同的特征类别将特征划分为不同的总体,接着检验不同总体之间均值是否相同。如果相同,那么这个特征就不能很好地解释因变量的变化。方差分析检验方法如下,计算每个特征的F统计量,接着按每个特征 F 值的大小进行排序,去除F值小的特征;
皮尔逊相关分析使用-1到1之间的数字来度量两个特征之间的相似性。接近1或-1的值表示这两个特征具有很高的相关性。要使用该方法进行特征选择,可以查看所有特征两两相关性的热点图(heatmap),在相关性高的“特征对”中保留与因变量(预测变量)具有最高相关性的特征。高相关与低相关的临界值取决于每个数据集中相关系数的范围。高相关性的范围一般是0.7以上;
信息增益分析基本方法如下:对于一个特征,计算模型有它和没它的时候信息量各是多少,两者的差值就是这个特征给模型带来的信息量(即增益)。通过对信息增益排名即可挑选出效果较好的变量。
包裹式(Wrapper)
包裹式特征选择使用特定的特征子集计算模型效能,该方法通过不断迭代不同的特征子集直到找到最佳解。其缺点是计算时间长,在样本量不够大的情况下模型容易产生过拟合。常见的包裹式特征选择方法有向后选择【10】、向前选择【10】、模拟退火算法【11】及遗传算法【12-13】。
向后选择从使用所有的数据集开始,该方法需要为每个特征与模型计算t检验或f检验的p值。然后,从模型中删除最不重要的特征(依据p值)。重复上述过程,直到模型中不重要特征被删除完毕为止;
向前选择从零个特征开始,对于每个单独的特征,该方法同样需要计算t检验或f检验的p值,然后选择p值最低的特征并将其添加到模型中。接下来,在保有第一个特征的条件下运行添加第二个特征的模型,并选择p值最低的第二个特征。以此类推,直到所有具有显著p值的特征都被添加到模型中;
遗传算法首先随机产生一批特征子集,并用评价函数给这些特征子集评分,然后通过交叉、突变等操作繁殖出下一代的特征子集,其中评分越高的特征子集被选中参加繁殖的概率越高。这样经过N代的繁殖和优胜劣汰后,种群中就可能产生评价函数值最高的特征子集;
模拟退火算法目标是要解决局部最优解困境。在随机产生特征子集后,该算法以一定的概率接受一个比当前模型效能要差的模型效能(这个概率随着时间的推移逐渐降低),这样做可以提高模型跳出局部最优解的可能性,从而达到全局最优解。
嵌入式(Embedded)
嵌入式方法将特征选择作为模型创建过程的一部分。该方法通常为前面两种选择选择方法的折衷。其中Lasso、岭回归【14】及决策树【15-16】是较为常见的嵌入式特征选择方法。
当希望能在最终模型中保留所有特征,但又不希望模型过于关注任何一个系数时,岭回归可以通过对模型的系数(权重)施加惩罚来做到这一点。具体操作是通过在回归的成本函数中添加一个惩罚项(L2正则项)来对系数过大进行惩罚。所有变量的权重共用一个参数lambda(λ)来对其进行惩罚,lambda是一个介于0和无穷大之间的值。lambda越高,系数收缩的越多(惩罚越大)。当lambda等于0时,结果将是一个不带惩罚项的普通最小二乘模型;与岭回归非常相似,Lasso回归是另一种惩罚模型系数(即变量权重)的方法(惩罚项为L1正则项)。与岭回归的区别是,Lasso趋向于使一部分变量的权重变为0,这将使得模型的特征数量减少,从而降低复杂性,这就是为什么Lasso在某些时候更受欢迎;第三种常用的嵌入式特征选择方法是决策树,它可以是回归树,也可以是分类树,具体取决于因变量是连续的还是离散的。在建立树模型时,函数内置了几种特征选择方法,在每次拆分时,用于创建树的函数会尝试对所有特征进行所有可能的组合。简单地说,它选择最能预测树中每个节点的最优特征。而在预测因变量时,最重要的特征在树的根(开始)附近进行拆分,而较不相关的特征是在树的叶(结束)附近进行拆分。生成树之后,可以选择“修剪”一些不向模型提供任何附加信息的节点。这可以防止过拟合,通常通过测试集的交叉验证来实现。
常见的特征选择方法总结如下:
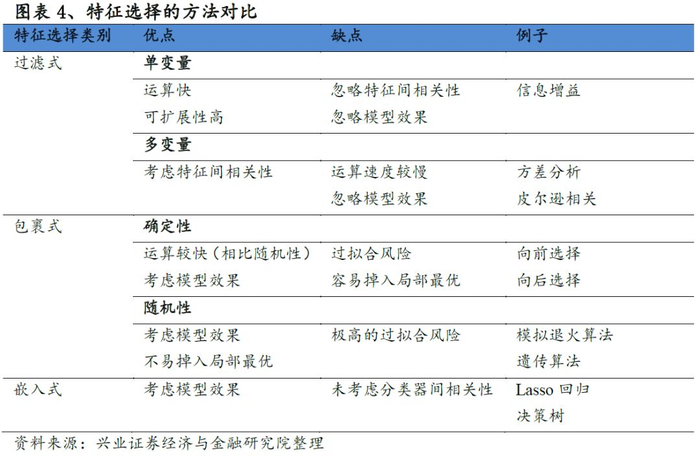
2.2.3 特征选择Vs特征提取比较
特征提取和特征选择都属于数据降维的方法。两者主要的不同在于特征提取是在原有特征基础之上去创造出一些新的特征出来,而特征选择则只是在原有特征上进行筛选。因此在数据的解释层面上特征选择能较好的保有原始数据的特征。

通过对特征选择和特征提取的整体分析,我们认为特征选择更加适合选股领域的分析,解释性和接受程度也更高。在特征选择里面,我们首先通过Filter限制变量的个数,进一步通过Wrapper确定最终的选股变量。
三、基于Filter&Wrapper的动态线性选股模型构建
3.1
数据准备&整体流程
为了避免行业市值的影响,我们对于每个因子都会做行业市值中性化,处理方法如下:以中信一级行业为标准,以每个行业内所有股票的流通市值中位数为界来进行大小票的划分,中位数以上者为该行业的大盘股,以下者视为该行业小盘股。而后分别在每个行业市值股票池内进行横截面因子的分位数变换标准化。除了因子层面的标准化之外,对于收益率我们同样通过分位数变换标准化的方式进行处理,以保证可比性。所以后续回归中的收益率均是标准化后的结果。
我们在因子体系构建的时候先用Filter的方法通过考虑因子表现和相关性,将因子数目控制在一定范围内;然后用Wrapper方法(我们这里采用逐步倒向线性回归的方式筛选,后面会有详细介绍)进一步优化因子数目。
在运用Filter以及Wrapper选择每期(比如月度选择)的有效因子后,我们运用线性回归的方式来构建最终的线性多因子模型,而这也使得我们保持了从特征选择到预测模型所使用的方法的统一性(Wrapper使用的就是线性回归)。我们将通过上述一整套流程得到的线性复合因子称作动态线性因子(Dynamic Linear Signal,DLS)。
3.2
动态因子选择
兴业证券金融工程团队所构建的因子库共计包含165个量化选股指标,进一步细分为价值、成长、质量、分析师情绪、动量反转、另类这六大类指标,其中另类进一步分为:规模、风险、流动性、技术这四个子类(部分因子定义参见附录)。

以上六大类165个因子是我们初始因子池。我们的目标是在每个月月底通过Filter&Wrapper方法选择有效的因子,接下来我们详细介绍两者的实现方法。Filter和Wrapper中方法众多,我们这里以Filter中的皮尔逊相关系数筛选法以及Wrapper中逐步倒向线性回归法为例阐述因子筛选的流程。
3.2.1 Filter筛选
1.选择每类中表现优秀的因子:
滚动计算过去5年每个因子的ICIR表现,从六大类别中分别选择表现最优秀的30%的因子;
2.剔除相关性高的因子:
在筛选时刻计算过去5年因子IC时间序列的两两相关性,删除相关性高于0.75的一对因子中的某一个。在删除的同时需要满足两个准则:i)、一旦确定高相关性因子对之后,要删除相应时点两个因子中过去5年ICIR表现差的因子;ii)、在删除的同时需保证每大类里面至少保留一个因子(以避免风格有偏);
从结果来看,经过第一步筛选之后我们的因子总量从165降至51个,具体参见图表-7(这里需要注意,由于表现好坏的筛选是一个固定的阈值,所以每期的结果一致)。而经过相关性筛选后因子总数稳定在32左右(具体参见图表-8);而每类选择的数目变动趋势参见图表-9。
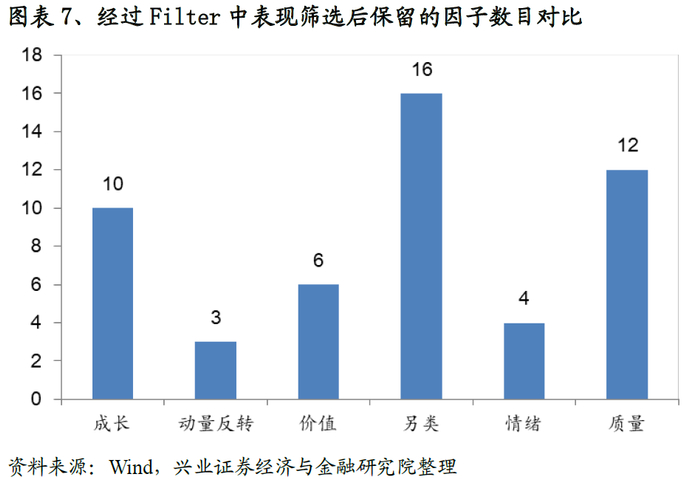
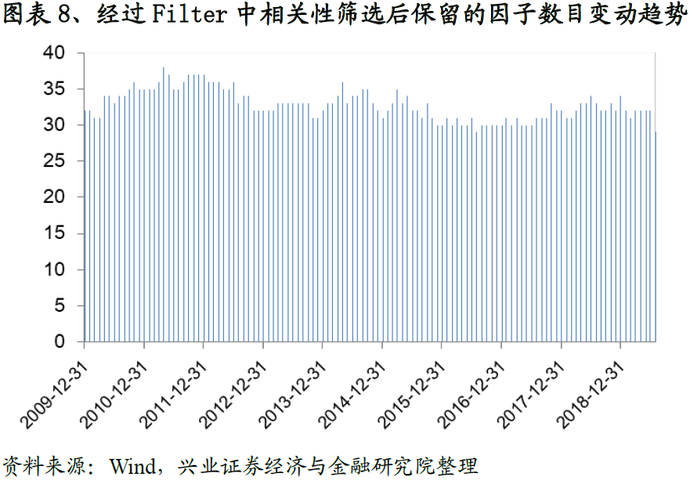
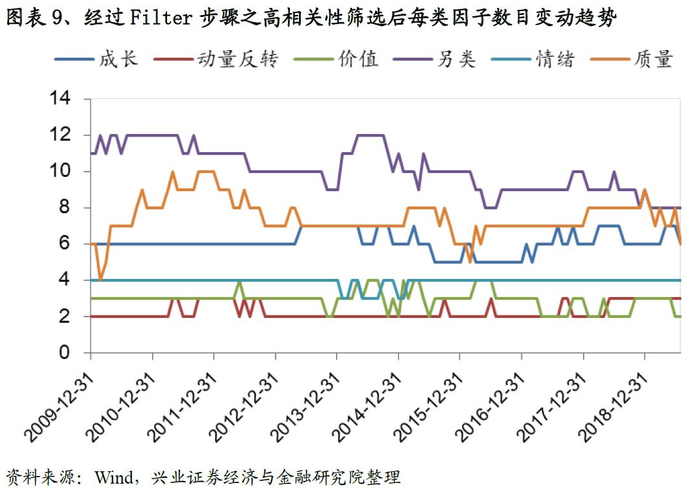
3.2.2 Wrapper筛选
在完成Filter步骤后,我们进一步通过Wrapper筛选剩余的因子。Wrapper有多种实现方式,这里我们采用的是逐步倒向线性回归的方式(与最后利用线性回归构建预测模型保持一致)来挑选因子。逐步倒向回归需要设定因子表现好坏的标准,我们这里以回归系数的P值作为参考,阈值设定为0.05,具体流程和注意事项如下:
1.为保证算法的稳定性,我们用过去3年36个月月底的横截面数据来构建训练样本。自变量为当期选中的因子过去三年的月度数据,Y为过去3年标准化的月度收益;
2.期初回归时,将截面选中因子全部放进去进行回归,如果所有因子P值都能达到要求,则程序终止,否则将表现最差因子剔除,同时以剩余因子为自变量再回归,重复该步骤,直至所有因子P值均满足要求;
3.这里需要注意的是,在剔除因子过程中,P值并不是唯一的参考标准,我们需要保证每大类中至少有一个因子存在。这也就意味着,如果在某次倒向回归中,某个类仅仅剩余一个因子,同时P值不达预期,此时即便该因子是表现最差的也不能删除,而这次回归只能追求次优解。这一限制的目的与前面Filter步骤中删除高相关性因子时所需要注意的地方是一致的,目的都是为了保证所选因子在大类风格上分布的均衡性。
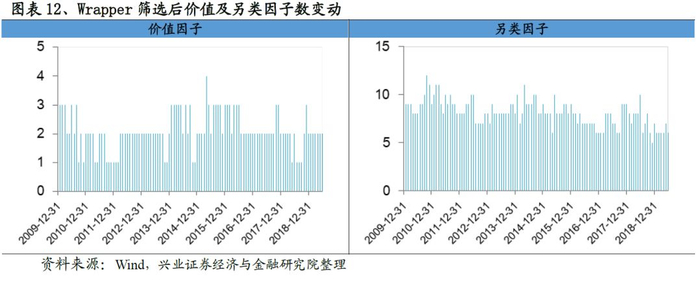
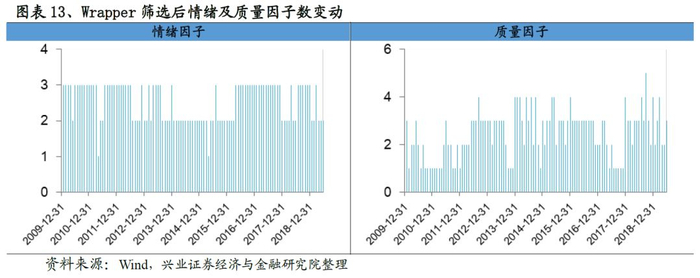
在完成Wrapper筛选后,我们每期保留的因子数大幅度下降,从Filter筛选后平均32个左右降低至18个的水准。观察每类因子的数目变动趋势,我们发现成长、动量反转变动最小,数目也最少,而质量和另类因子的数量变动幅度最大。
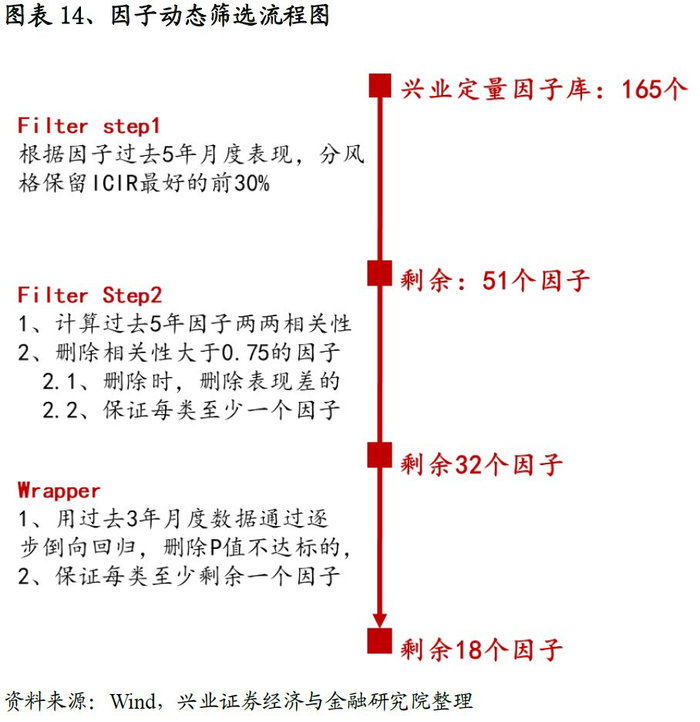
最终我们带着经过Filter&Wrapper筛选后的因子进入到下一个环节,用线性回归的方式构建多因子收益率预测模型。完整的Filter&Wrapper筛选流程参见图表-14。
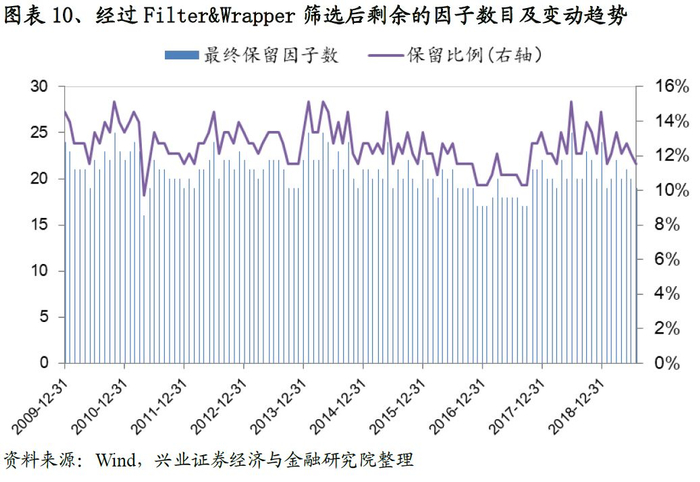
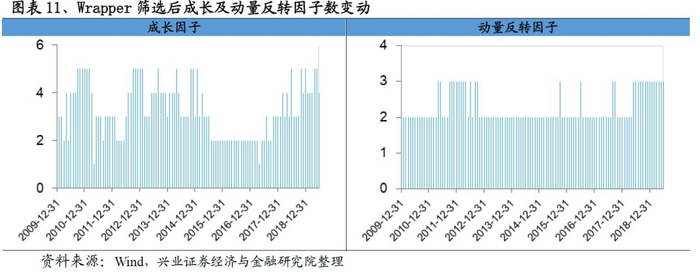
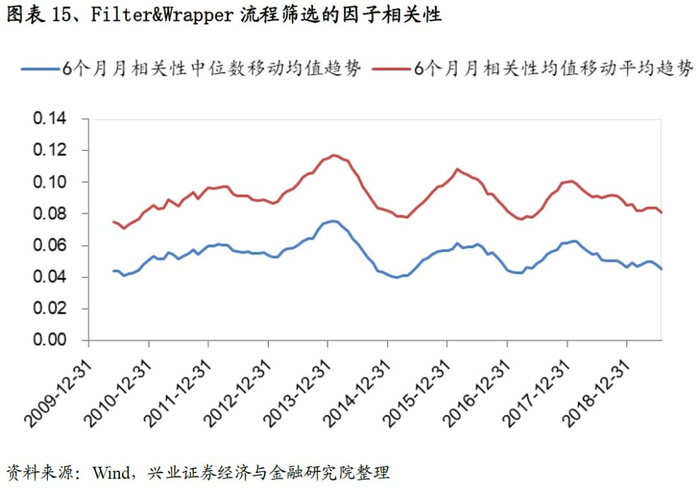
我们研究Filter&Wrapper流程截面筛选的因子相关性,从结果来看,每期因子的相关性非常低,均值稳定在0.045左右。因子相关性较低一方面提升最终合成因子的稳定性同时规避了多重共线性等问题,为后续的研究打下基础。
3.3
DLS因子表现分析
经过动态因子选择环节,我们确定了每期选中的因子,进一步通过线性回归的方式将因子合成。同时为了保证算法的稳定性,与前面一致,我们用选中的因子过去3年36个月月底的横截面数据来构建回归样本,并通过最小二乘回归确定回归系数,进而得到最终的复合因子DLS(Dynaimc Linear Signal)
3.3.1 DLS全市场表现分析
IC以及分位数测试结果显示该因子的选股能力非常强:IC均值达到10.6%,ICIR达到1.50;而多空年化收益率达到43.0%、夏普率高达4.99。

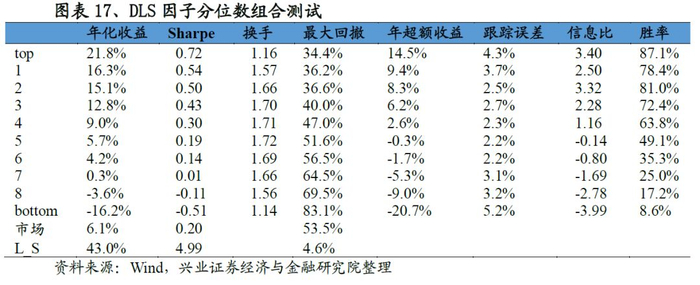
3.3.2 DLS与基准模型的对比分析
前文详细描述了DLS因子的构建方式,这里我们尝试通过较为简单的方法为DLS因子构建一个基准模型,并对两者进行对比分析。基准模型的构建方法如下:在某个时刻,计算过去5年所有165个因子表现,从每个类里面选择最为有效(ICIR)的3个因子(这一步亦是Filter的第一步;而每类选择3个也保证了最终因子总量和DLS所选择的因子数量基本一致)等权合成,称之为Benchmark Model(BM)。
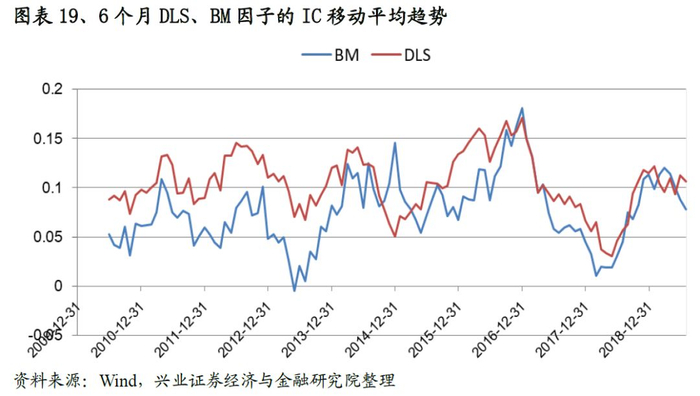
从同时期的IC以及分位数组合测试结果来看:DLS因子的IC均值达到0.106,ICIR以及T值分别为1.50、16.05,远高于BM相应指标的水准。从IC的移动平均趋势也可以看出DLS的有效性要远高于BM因子;同样,DLS的多空年化收益率以及夏普率分别为43.0%,4.99,也优于基准因子的表现。
为了进一步考察DLS的表现,我们还构建了一个在已知全样本因子表现下的复合因子Future_Sig:回测2009年12月31日-2019年7月底所有因子的月度ICIR,然后每类中选择月均ICIR最高的3个因子并等权合成。该因子无论是IC亦或是多空表现都非常优异。但需要注意的是,Future_Sig是站在2019年7月31日,观察并选择在整个历史样本区间上表现最优的因子,而这实际上这是严重的窥探未来数据的做法。当然通过参考Future_Sig因子构建方法以及对比Future_Sig与DLS因子表现我们可得知:1、DLS因子构建方法没有利用任何未来信息(均是站在当前时点回望过去一段时间的表现);2、DLS因子与Future_Sig的表现非常接近,也在一定程度上说明了上述动态因子选择方法的有效性。

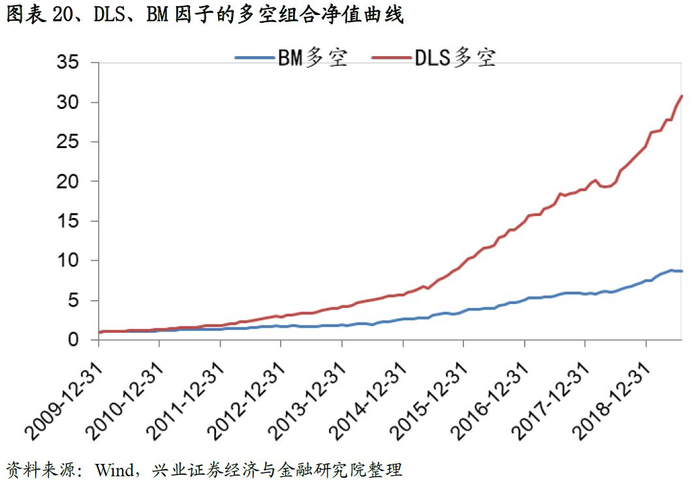
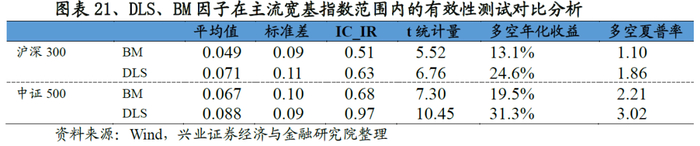
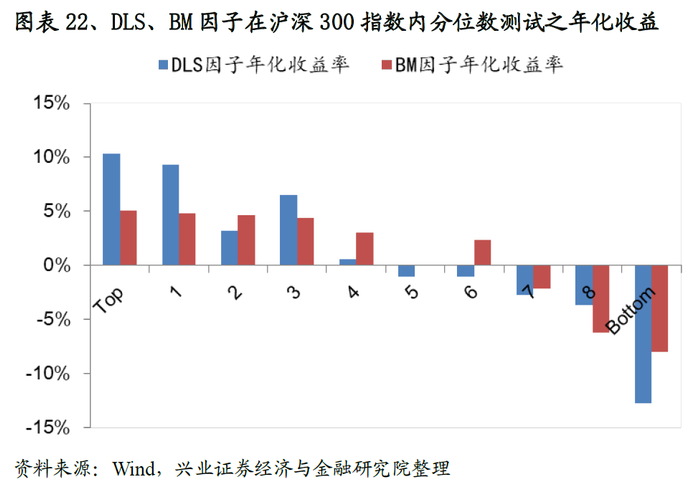
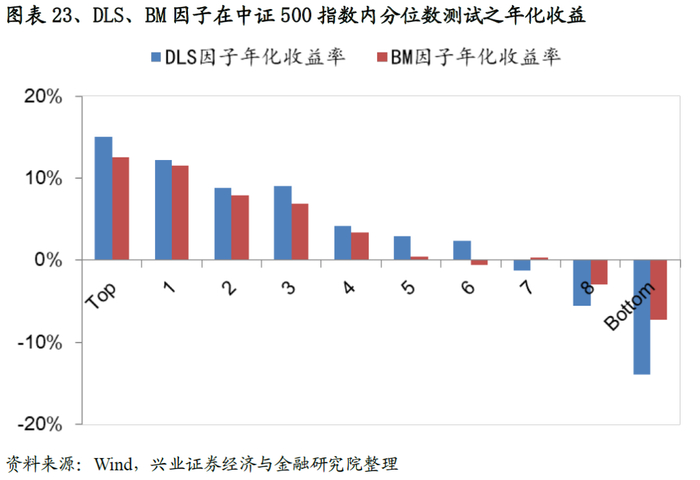
3.3.3 DLS在宽基指数成分股内的表现分析
我们将股票池缩小至主要宽基指数范围内(沪深300/中证500),从测试结果来看,DLS因子的有效性和稳定性规律依然不变,以在中证500测试为例:DLS因子IC、ICIR、T值分别达到0.88、0.97、10.45,多空组合年化收益率31.3%,夏普率3.02,大幅度优于基准的表现,且各组别的单调性要优于基准因子的表现。
3.4
A-DLS因子表现分析
整个DLS因子的构建逻辑(包括Filter & Wrapper的因子筛选流程)都是假设因子和收益之间的关系是线性的,因此那些具有非线性选股能力的因子将会被全部剔除。为了能够更好地将非线性预测能力与上述模型融为一体,我们引入了在《基于集成学习算法的量化选股模型研究》中所构建的集成学习因子(基于改进版的Adaboost算法)。如何将DLS与集成学习因子结合起来呢?这里大致有两种思路:
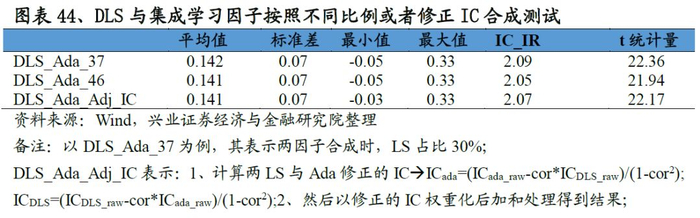
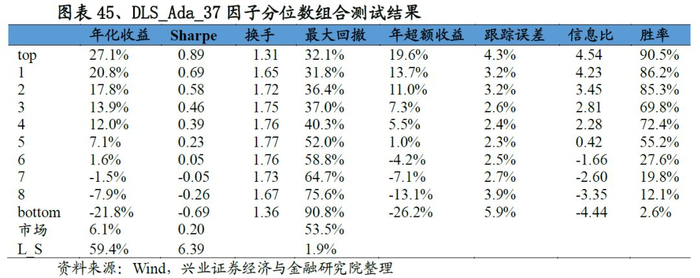
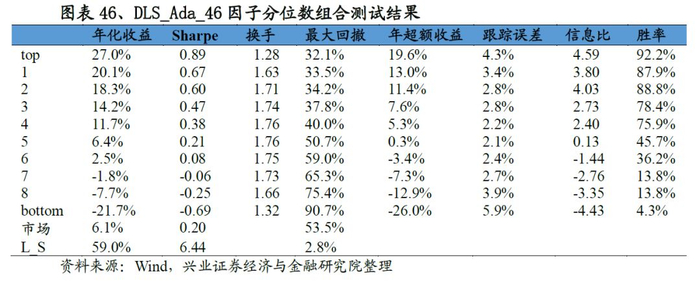
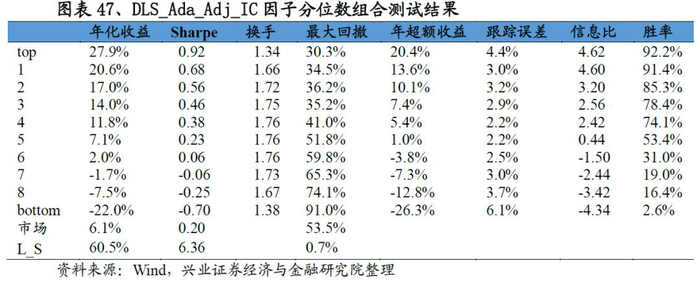
1.将DLS与集成学习因子分别当成两个因子,通过等权、经验比例、相关性调整IC(附录有详细介绍)加权等方式将两个因子合成;
2.将集成学习因子作为一个体现非线性选股能力的单因子,与Filter&Wrapper选择的因子一起进行线性回归,并得到最终的复合因子。
我们对上述两种方式都进行了实证分析,这里重点呈现第二种方式(第一种方法的结果请参见附录1),并把利用该方法生成的因子称为A-DLS (Adaboost &Dynamic Linear Signal)。注意在构建A-DLS因子时,所有方法和细节处理均保持不变,只是在每期回归时,多增加了一个集成学习因子。
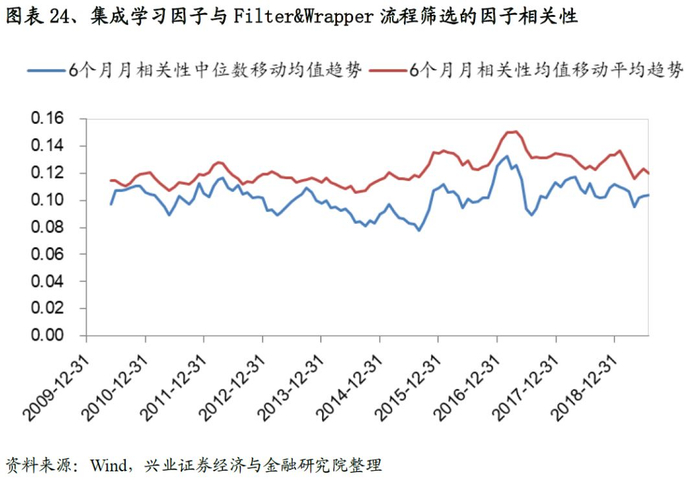
同时我们证实了集成学习因子与前面Filter&Wrapper筛选的因子相关性非常低,均值稳定在0.1左右。低相关性进一步支持将集成学习因子纳入我们的回归模型当中。
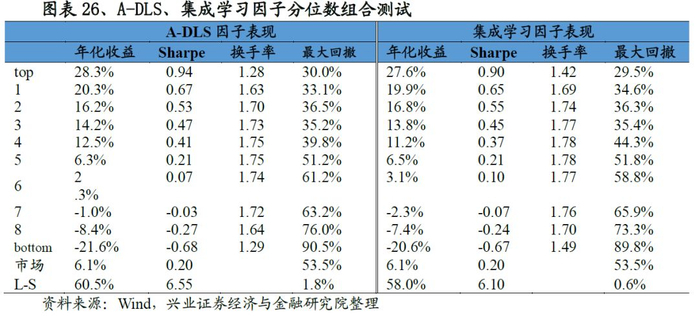
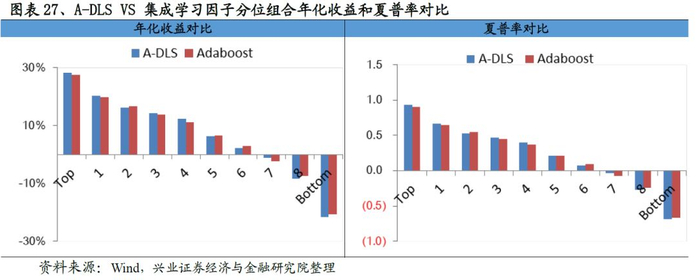
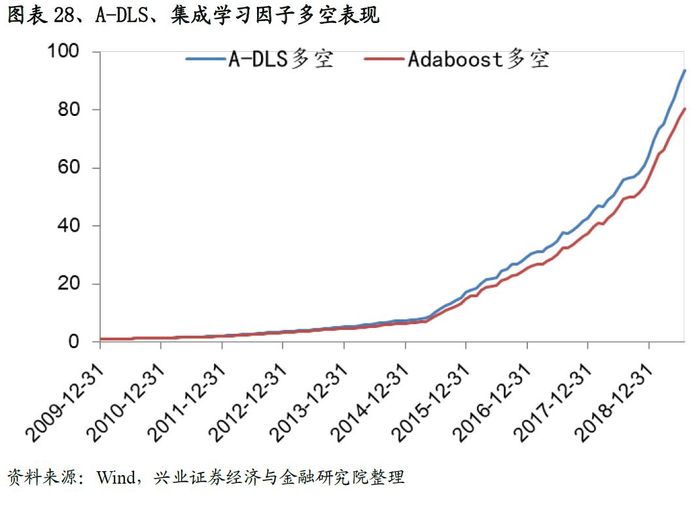
从最终合成因子的测试结果来看,A-DLS因子的表现十分优秀:从IC来看,A-DLS因子IC均值、ICIR以及T值分别为0.141、2.01和21.58;从分位数组合测试来看,A-DLS因子多空组合年化收益率高达60.5%、夏普率达到6.55,且A-DLS因子各分为组合的单调性、换手率均优于集成学习因子的表现。整体来看A-DLS表现略胜一筹。

四、基于A-DLS因子的选股策略研究
一般而言,投资者会结合自己的需求(如投资风险偏好不同、资金容量要求不同、换手频率不同等)构建不同风格的投资策略。接下来我们基于A-DLS因子构建主动量化以及增强选股策略。
4.1
主动量化策略构建
基于A-DLS因子我们构建了主动量化选股模型:
1.每期选择100只股票,以中证500作为业绩比较基准;
2.调仓日:若当期持仓的股票下一期没有跌出前200,仍然继续持有;
3.其他设定:选股池需删除ST、同时保证上市天数满180天;交易成本双边0.3%。
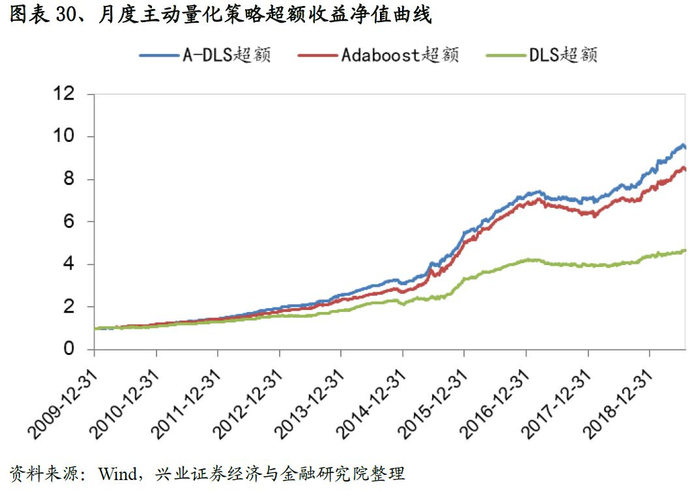
从测试结果来看,我们基于A-DLS因子构建的主动量化策略成绩斐然,策略多头超额收益风险比为4.61,最大回撤为6.6%。

4.2
指数增强选股策略构建
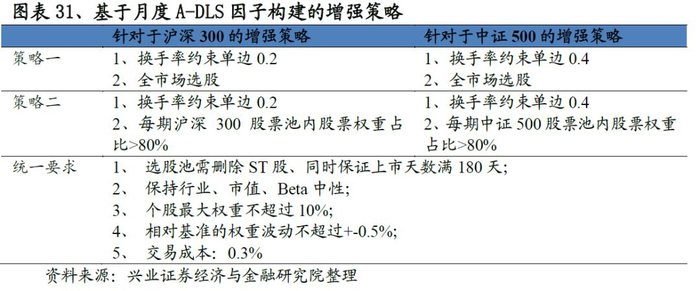
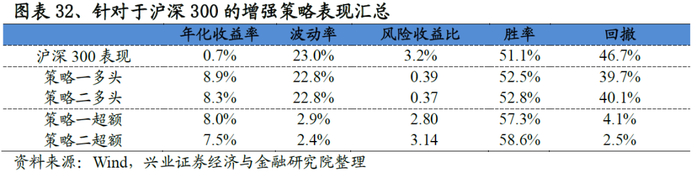
指数增强策略旨在控制跟踪误差的前提下,尽可能获取超越基准的表现。综合考虑投资者的偏好,针对于沪深300以及中证500宽基指数,我们构建了2个增强模型,不同模型的实现细节参见图表32。
4.2.1 基于A-DLS因子的沪深300增强策略
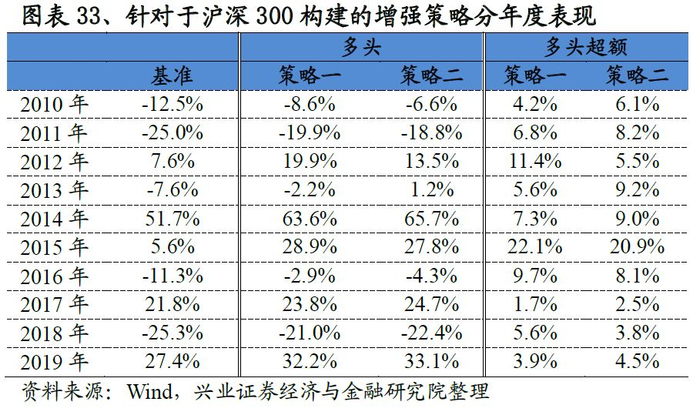
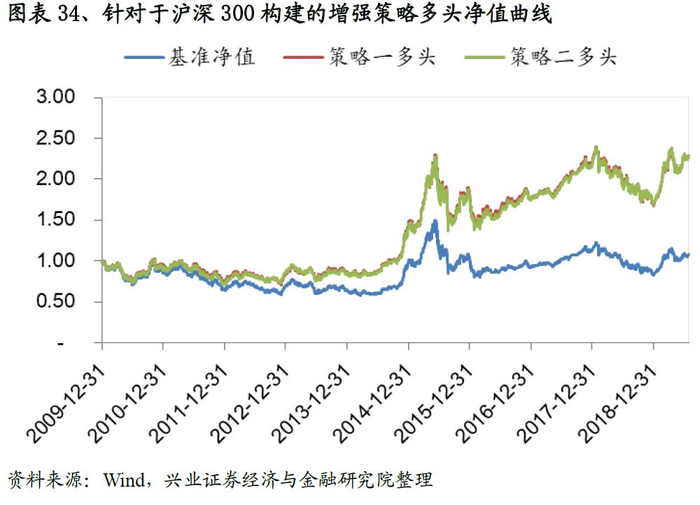
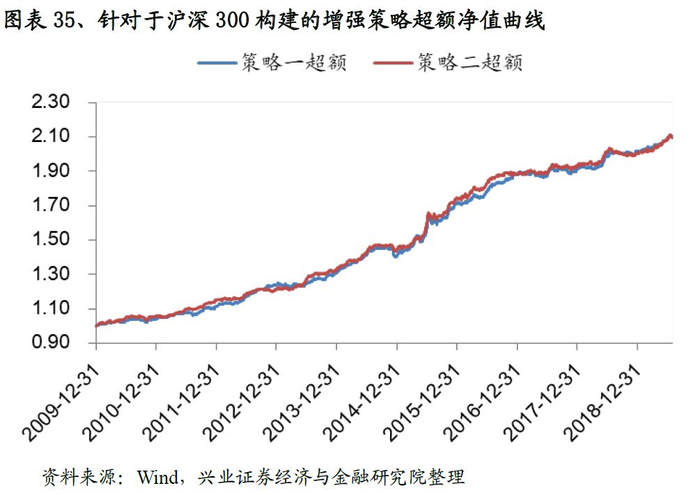
基于沪深300的增强策略表现非常优异,以策略二为例:策略相对沪深300指数的年化超额收益稳定在7.5%左右,最大回撤为2.5%,风险收益比高达3.14。分年度来看,选股策略在每一年均能稳定的跑赢基准,2019年以来(截至7月31日)超额收益稳定在4.5%。
同时我们发现策略一和策略二表现非常接近,这实际上意味着:沪深300具有非常鲜明的市值、行业、Beta特点,只要这三类风格做到相对中性,那么即便不添加沪深300成分股权重占比80%以上的要求,策略依然可以做到稳定的跟踪沪深300的表现。
4.2.2 基于A-DLS因子的中证500增强策略
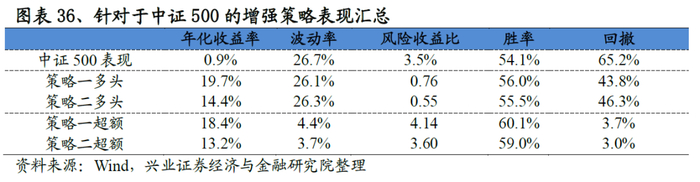
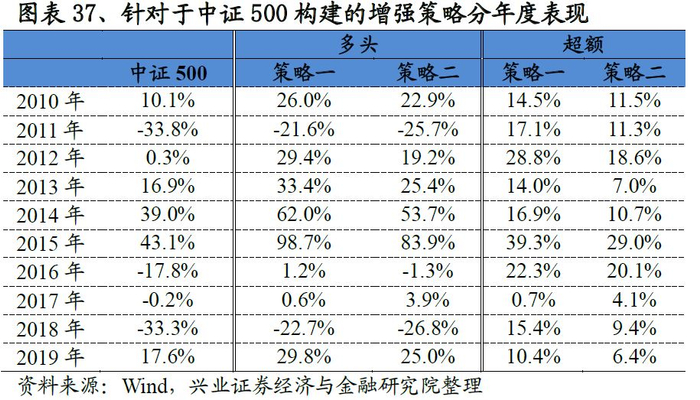
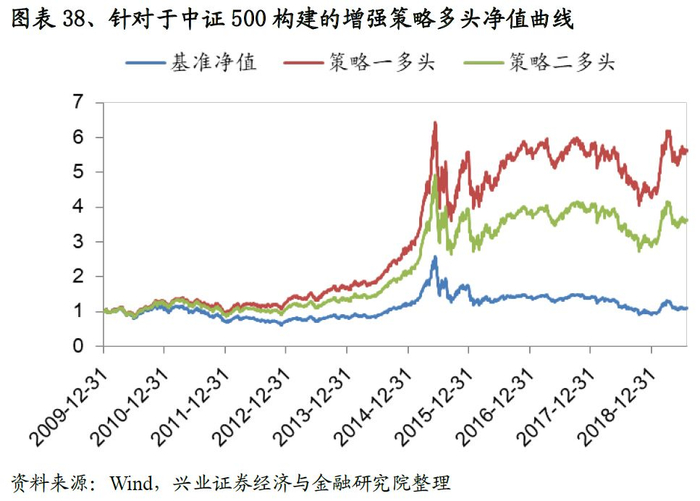
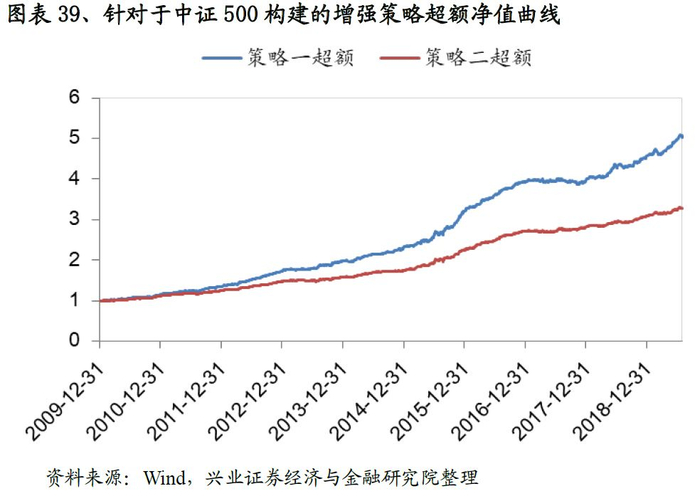
与沪深300的增强策略框架一致,我们构建了中证500指数增强策略。从结果来看策略表现突出,以策略一为例:策略年化超额收益率高达18.4%,收益风险比达到4.14,回撤为3.7%。分年度来看,各策略也能稳定的战胜基准,2019年以来策略一、策略二分别战胜基准10.4%、6.4%个点。
五、总结
本文的研究主要聚焦于两个方面展开:1、借鉴机器学习中特征选择的方法,在不窥探未来数据的情况下构建了一套完整的动态因子选择方法,并验证了该方法的有效性;2、尝试将非线性因子与线性模型相融合,进一步构建完整的选股体系。回顾我们的机器学习系列研究,每个系列侧重解决的问题不尽相同:
1.在2015年初-2016年的5篇系列里面,我们详细的介绍了各个机器学习模型的优缺点,以及在选股领域的应用尝试。该系列更多的是让大家对机器学习在选股领域有一个初步的认知;
2.在《基于集成学习算法的量化选股模型研究》中,我们以Adaboost为基础,详细探讨了机器学习和选股结合的一系列深度问题:机器学习的可解释性、过拟合问题、低换手大容量模型、高换手模型等等,更加具有针对性和落地意义;
3.本篇报告,我们聚焦于机器学习的前序篇章:因子选择问题。通过将特征选择引入进来,层层递进,我们构建了一个完整的因子选择体系。
文章最后还是回到研究的初衷:人工智能在量化投资领域的应用之路也许不会一帆风顺,但我们的努力绝不会停止,我们将坚守卖方研究的初衷,砥砺前行,争取为大家提供更多有价值的成果。
六、增强策略今年以来表现
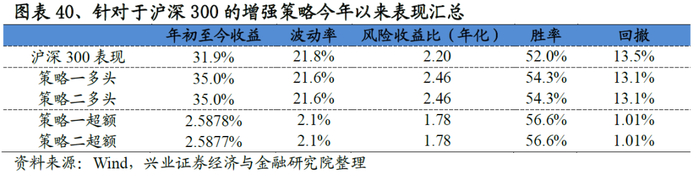
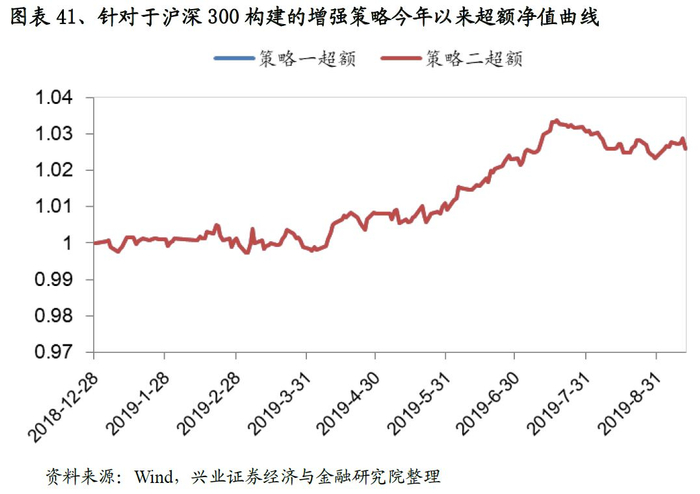
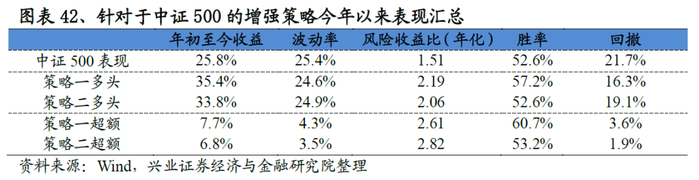
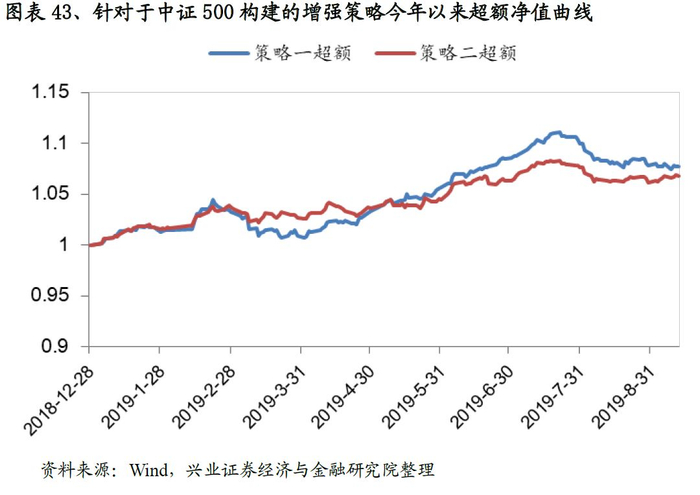
我们统计了2019年1月1日-2019年9月12日期间指数增强策略的表现,从结果来看:针对于沪深300的增强策略今年以来的超额收益稳定在2.6%,最大回撤1%;针对于中证500的增强策略有一定差异,其中策略二今年以来的超额收益稳定6.8%,最大回撤1.9%。各增强策略表现优异。
七、附录
7.1
部分中间测试结果
DLS与集成学习因子合成测试
参考文献
【1】R. E. Bellman, “Dynamic Programming, Princeton University Press,” Princeton, NJ, USA, 1957.
【2】J. Han, “Data Mining: Concepts and Techniques,” Morgan Kaufmann Publishers, San Francisco, Calif, USA, 2005.
【3】D. M. Strong, Y.W. Lee, and R. Y. Wang, “Data quality in context,” Communications of the ACM, vol. 40, no. 5, pp. 103–110, 1997.
【4】Y. Saeys, I. Inza, and P. Larra˜naga, “A review of feature selection techniques in bioinformatics,” Bioinformatics, vol. 23, no. 19, pp. 2507–2517, 2007.
【5】A. L. Blum and P. Langley, “Selection of relevant features and examples in machine learning,” Artificial Intelligence, vol. 97,no. 1-2, pp. 245–271, 1997.
【6】S. Das, Filters, “Wrappers and a boosting-based hybrid for feature selection,” in Proceedings of the 18th International Conference on Machine Learning (ICML ’01), pp. 74–81, Morgan Kaufmann Publishers, San Francisco, Calif, USA, 2001.
【7】C. Ding and H. Peng, “Minimum redundancy feature selection from microarray gene expression data,” in Proceedings of the IEEE Bioinformatics Conference (CSB ’03), pp. 523–528, IEEE Computer Society,Washington, DC, USA, August 2003.
【8】M. A. Hall, “Correlation-based feature selection for machine learning,” Tech. Rep., 1998.
【9】P.Yang, B. B. Zhou, Z. Zhang, and A. Y. Zomaya, “Amulti-filter enhanced genetic ensemble system for gene selection and sample classification of microarray data,” BMC Bioinformatics, vol. 11, supplement 1, article S5, 2010.
【10】H. Glass and L. Cooper, “Sequential search: a method for solving constrained optimization problems,” Journal of the ACM, vol. 12, no. 1, pp. 71–82, 1965
【11】Van Laarhoven P J M, Aarts E H L. “Simulated annealing: Theory and applications,” Springer, Dordrecht, 1987: 7-15.
【12】T. Jirapech-Umpai and S. Aitken, “Feature selection and classification for microarray data analysis: evolutionary methods for identifying predictive genes,” BMC Bioinformatics, vol. 6, article 148, 2005.
【13】C. H.Ooi and P. Tan, “Genetic algorithms applied tomulti-class prediction for the analysis of gene expression data,” Bioinformatics, vol. 19, no. 1, pp. 37–44, 2003.
【14】S. Ma, X. Song, and J. Huang, “Supervised group Lasso with applications to microarray data analysis,” BMC Bioinformatics, vol. 8, article 60, 2007.
【15】R. D´ıaz-Uriarte and S. Alvarez de Andr´es, “Gene selection and classification of microarray data using random forest,” BMC Bioinformatics, vol. 7, article 3, 2006.
【16】H. Jiang, Y. Deng, H.-S. Chen et al., “Joint analysis of two microarray gene-expression data sets to select lung adenocarcinoma marker genes,” BMC Bioinformatics, vol. 5, article 81, 2004.
【17】Saeys Y, Inza I, Larrañaga P., “A review of feature selection techniques in bioinformatics,” bioinformatics, 2007, 23(19): 2507-2517.
【18】Jolliffe I. ,“Principal component analysis,” Springer Berlin Heidelberg, 2011.
【19】Hyvärinen A, Oja E. ,“Independent component analysis: algorithms and applications,” Neural networks, 2000, 13(4-5): 411-430.
【20】Kruskal J B, Wish M. ,“Multidimensional scaling,” Sage, 1978.
【21】B. Scholkopf , A. Smola , and K.R. Muller. ,“Nonlinear component analysis as a kernel eigenvalue problem,” Neural Computation, 10(5): 1299- 1319, 1998
【22】J. B. Tenenbaum , V. de Silva, and J. C. Langford, “A global geometric framework for nonlinear dimensionality reduction,” Science, 290, pp. 2319 - 2323, 2000
【23】Sam T. Roweis , and Lawrence K. Saul, “Nonlinear Dimensionality Reduction by Locally Linear Embedding,” Science 22 December 2000
【24】Mikhail Belkin , Partha Niyogi ,“Laplacian Eigenmaps for Dimensionality Reduction and Data Representation,” Computation , 2003
【25】Xiaofei He, Partha Niyogi, “Locality Preserving Projections,” Advances in Neural Information Processing Systems 16 (NIPS 2003), Vancouver, Canada, 2003
风险提示:文献中的结果均由相应作者通过历史数据统计、建模和测算完成, 在政策、市场环境发生变化时模型存在失效的风险。
注:文中报告节选自兴业证券经济与金融研究院已公开发布研究报告,具体报告内容及相关风险提示等详见完整版报告。
证券研究报告:《当线性模型遇见机器学习》。
对外发布时间:2019年9月17日
报告发布机构:兴业证券股份有限公司(已获中国证监会许可的证券投资咨询业务资格)


